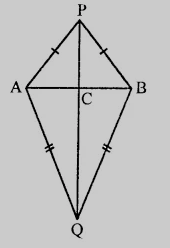
$AB$是一条线段，$P$和$Q$是$AB$两侧的点，它们到点$A$和$B$的距离相等。证明直线$PQ$是$AB$的垂直平分线。

已知

$AB$是一条线段，$P$和$Q$是$AB$两侧的点，它们到点$A$和$B$的距离相等。

目标

我们必须证明直线$PQ$是$AB$的垂直平分线。

解答

在$\triangle PAQ$和$\triangle PBQ$中，

$PA = PB$ (已知)

$QA = QB$ (已知)

$PQ = PQ$ (公共边)

因此，根据SSS公理，

$\triangle PAQ \cong \triangle PBQ$

这意味着，

$\angle APQ = \angle BPQ$ (全等三角形对应角相等)

在$\triangle APC$和$\triangle BPC$中，

$PA = PB$ (已知)

$\angle APC = \angle BPC$

$PC = PC$ (公共边)

因此，根据SAS公理，

$\triangle APC \cong \triangle BPC$

这意味着，

$AC = BC$ (全等三角形对应边相等)

$\angle PCA = \angle PCB$ (全等三角形对应角相等)

$\angle PCA + \angle PCB = 180^o$ (邻补角)

这意味着，

$\angle PCA = \angle PCB = 90^o$

因此，$PQ$是$AB$的垂直平分线。

证毕。

Tutorialspoint

更新于：2022年10月10日

浏览量：53

开启你的职业生涯

完成课程获得认证

开始学习