给定一条线段$\overline{\mathrm{AB}}$，其长度未知，作$\overline{\mathrm{PQ}}$使得$\overline{\mathrm{PQ}}$的长度是$\overline{\mathrm{AB}}$的两倍。

已知

一条线段$\overline{AB}$。

要求

我们必须构造$\overline{PQ}$，使得$\overline{PQ}$的长度是$\overline{AB}$的两倍。

解法

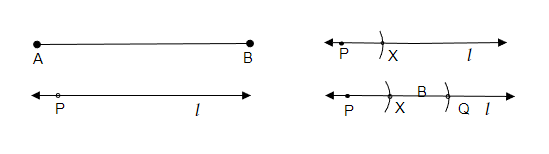
作图步骤：

(i) 作线段$\overline{PQ}$。

(ii) 将圆规的一端放在已知线段AB的A点上，调整圆规到$\overline{AB}$的长度。

(iii) 作一条直线'l'，并在直线上取一点P。

(iv) 现在，将圆规的一端放在P点上，在直线'l'上截取一段，标记为X。

(v) 再次将圆规的一端放在X点上，在直线'l'上作另一个弧，标记为Q。

(vi) 因此，所需的线段$\overline{PQ}$就形成了。

教程点

更新于：2022年10月10日

56 次浏览

开启您的职业生涯

完成课程获得认证

开始学习