在问题 4 中，点\( \mathrm{C} \) 被称为线段\( \mathrm{AB} \) 的中点。证明每条线段都只有一个中点。

已知

点 $C$ 是 $\overline{AB}$ 的中点。

要做的

我们必须证明每条线段都只有一个中点。

解决方案


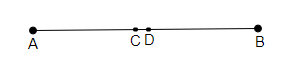
假设点 $C$ 和 $D$ 是 $\overline{AB}$ 的两个中点。

由于，$C$ 和 $D$ 是 $\overline{AB}$ 的中点。

我们得到，

$AC=CB$ 和 $AD=BD$

根据欧几里得公理

我们得到，

$AC+CB=AB$  (因为，$AC+CB$ 与 $AB$ 重合)

类似地，我们得到，

$AD+BD=AB$  (因为，$AD+BD$ 与 $AB$ 重合)

现在， 

在 $AC=CB$ 的两边加上 $AC$

我们得到，

$AC+AC=CB+AC$ (因为，如果相等的东西加到相等的东西上，那么整体也是相等的。)

这意味着，

$2AC=AB$...........(i)

以类似的方式，我们得到，

$AD+AD=DB+AD$  (因为，如果相等的东西加到相等的东西上，那么整体也是相等的。)

这意味着，

$2AD=AB$.............(ii)

从 (i) 和 (ii)

我们得到 RHS 相同 

因此，

让我们将 (i) 和 (ii) 的 LHS 等价

我们得到，

$2AC=2AD$ (根据欧几里得公理：等于同一事物的事物彼此相等。)

因此，

$AC=AD$(根据欧几里得公理：等于同一事物两倍的事物彼此相等。)

因此，

我们可以说点 $C$ 和 $D$ 是相同的点。

因此， 

我们假设 $C$ 和 $D$ 是两个不同的中点的假设是错误的。

因此，每条线段都只有一个中点。

证毕。

更新于： 2022 年 10 月 10 日

74 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告