电力电子 - 斩波器

---

---

斩波器使用高速连接和断开电源负载。通过连续触发功率开关的通/断，间歇地将固定直流电压施加到电源负载。功率开关保持通或断的时间段分别称为斩波器的通态时间和断态时间。

斩波器主要应用于电动汽车、风能和太阳能转换以及直流电机调速器。

斩波器的符号

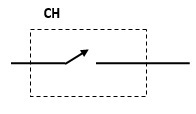
斩波器的分类

根据输出电压，斩波器可分为：

• 升压斩波器（升压转换器）
• 降压斩波器（降压转换器）
• 升/降压斩波器（降压-升压转换器）

升压斩波器

升压斩波器的平均输出电压 (V_o) 大于输入电压 (V_s)。下图显示了升压斩波器的配置。

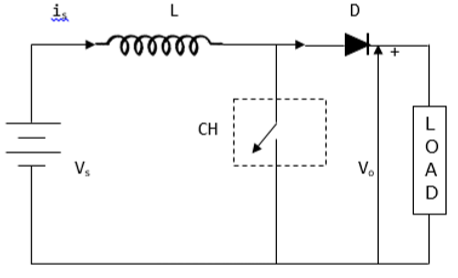
电流和电压波形

当斩波器接通时，V₀（平均输出电压）为正，当斩波器断开时为负，如下面的波形所示。

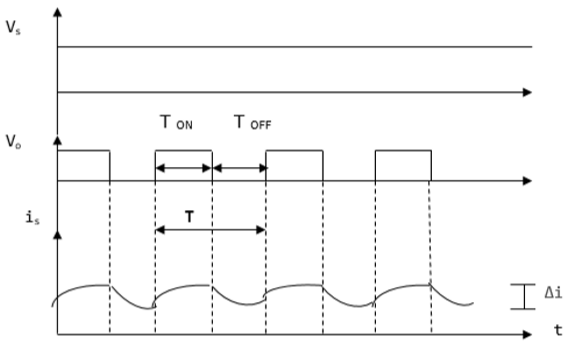
其中

T_ON – 斩波器接通的时间间隔

T_OFF – 斩波器断开的时间间隔

V_L – 负载电压

V_s – 源电压

T – 斩波周期 = T_ON + T_OFF

V_o 由下式给出：

$$V_{0}=\frac{1}{T}\int_{0}^{T_{ON}}V_{S}dt$$

当斩波器 (CH) 接通时，负载短路，因此，T_ON期间的输出电压为零。此外，在此期间电感充电。这使得 V_S = V_L

$L\frac{di}{dt}=V_{S},$ $\frac{\Delta i}{T_{ON}}=\frac{V_{S}}{L}$

因此，$\Delta i=\frac{V_{S}}{L}T_{ON}$

Δi = 电感峰峰值电流。当斩波器 (CH) 断开时，电感 L 发生放电。因此，V_s 和 V_L 的总和如下：

$V_{0}=V_{S}+V_{L},\quad V_{L}=V_{0}-V_{S}$

但是 $L\frac{di}{dt}=V_{0}-V_{S}$

因此，$L\frac{\Delta i}{T_{OFF}}=V_{0}-V_{S}$

这给出，$\Delta i=\frac{V_{0}-V_{S}}{L}T_{OFF}$

将通态的 Δi 与断态的 Δi 相等得到：

$\frac{V_{S}}{L}T_{ON}=\frac{V_{0}-V_{S}}{L}T_{OFF}$, $V_{S}\left ( T_{ON}+T_{OFF} \right )=V_{0}T_{OFF}$

$V_{0}=\frac{TV_{S}}{T_{OFF}}=\frac{V_{S}}{\frac{\left ( T+T_{ON} \right )}{T}}$

这给出平均输出电压为：

$$V_{0}=\frac{V_{S}}{1-D}$$

上述方程表明 V_o 可以从 V_S 变化到无穷大。它证明输出电压将始终大于输入电压，因此，它会提升或增加电压水平。

降压斩波器

这也被称为降压转换器。在这种斩波器中，平均输出电压 V_O 小于输入电压 V_S。当斩波器接通时，V_O = V_S，当斩波器断开时，V_O = 0

当斩波器接通时：

$V_{S}=\left ( V_{L}+V_{0} \right ),\quad V_{L}=V_{S}-V_{0},\quad L\frac{di}{dt}=V_{S}-V_{0},\quad L\frac{\Delta i}{T_{ON}}=V_{s}+V_{0}$

因此，峰峰值负载电流由下式给出：

$\Delta i=\frac{V_{s}-V_{0}}{L}T_{ON}$

电路图

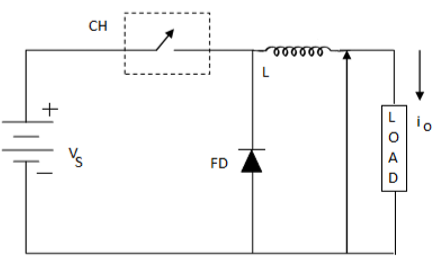
其中 FD 是续流二极管。

当斩波器断开时，电感发生极性反转和放电。电流通过续流二极管和电感流向负载。这给出：

$$L\frac{di}{dt}=V_{0}........................................\left ( i \right )$$

改写为：$\quad L\frac{\Delta i}{T_{OFF}}=V_{0}$

$$\Delta i=V_{0}\frac{T_{OFF}}{L}...................................\left ( ii \right )$$

联立方程 (i) 和 (ii) 得到：

$\frac{V_{S}-V_{0}}{L}T_{ON}=\frac{V_{0}}{L}T_{OFF}$

$\frac{V_{S}-V_{0}}{V_{0}}=\frac{T_{OFF}}{T_{ON}}$

$\frac{V_{S}}{V_{0}}=\frac{T_{ON}-T_{OFF}}{T_{ON}}$

上述方程给出：

$$V_{0}=\frac{T_{ON}}{T}V_{S}=DV_{S}$$

方程 (i) 给出：

$\Delta i=\frac{V_{S}-DV_{S}}{L}DT$, 由 $D=\frac{T_{ON}}{T}$

$=\frac{V_{S}-\left ( 1-D \right )D}{Lf}$

$f=\frac{1}{T}=$斩波频率

电流和电压波形

电流和电压波形如下：

对于降压斩波器，输出电压始终小于输入电压。这由下面的波形所示。

升/降压斩波器

这也被称为降压-升压转换器。它可以提高或降低输入电压水平。下图显示了一个降压-升压斩波器。

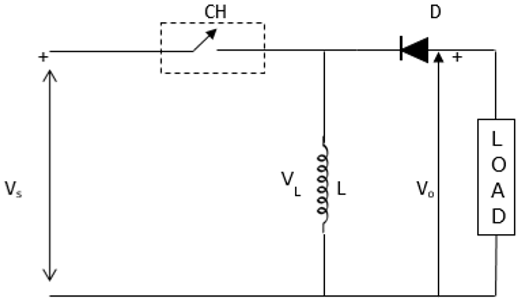
当斩波器接通时，电感 L 由源电压 V_s 充电。因此，V_s = V_L。

$$L\frac{di}{dt}=V_{S}$$ $$\Delta i=\frac{V_{S}}{L}T_{ON}=\frac{V_{S}}{L}T\frac{T_{ON}}{T}=\frac{DV_{S}}{Lf}$$

因为：

$D=\frac{T_{ON}}{T}$ 且 $f=\frac{1}{T} .............................................. \left ( iii \right )$

当斩波器断开时，电感的极性反转，这导致它通过二极管和负载放电。

因此，

$$V_{0}=-V_{L}$$ $$L\frac{di}{dt}=-V_{0}$$

$L\frac{\Delta i}{T_{OFF}}=-V_{0}$, 因此 $\Delta i=-\frac{V_{0}}{L}T_{OFF}................................\left ( iv \right )$

评估方程 (iii) 和 (iv) 得到：

$\frac{DV_{S}}{Lf}=-\frac{V_{0}}{L}T_{OFF}$, $DV_{S}=-DV_{S}=-V_{0}T_{OFF}f$

$DV_{S}=-V_{0}\frac{T-T_{ON}}{T}=-V_{0}\left ( 1-\frac{T_{ON}}{T} \right )$, $V_{0}=-\frac{DV_{S}}{1-D}$

因为 $D=\frac{T_{ON}}{T}=\frac{T-T_{OFF}}{1-D}$

这给出：

$V_{0}=\frac{DV_{S}}{1-D}$

D 可以从 0 变化到 1。当 D = 0 时；V_O = 0

当 D = 0.5 时，V_O = V_S

当 D = 1 时，V_O = ∞。

因此，在 0 ≤ D ≤ 0.5 的区间内，输出电压在 0 ≤ V_O < V_S 的范围内变化，我们得到降压或降压操作。而在 0.5 ≤ D ≤ 1 的区间内，输出电压在 V_S ≤ V_O ≤ ∞ 的范围内变化，我们得到升压或升压操作。