PyTorch 快速指南

---

---

PyTorch - 简介

PyTorch 定义为一个用于 Python 的开源机器学习库。它用于自然语言处理等应用程序。它最初由 Facebook 人工智能研究小组开发，Uber 的概率编程软件 Pyro 也基于它构建。

最初，PyTorch 由 Hugh Perkins 开发，作为基于 Torch 框架的 LusJIT 的 Python 包装器。PyTorch 有两个变体。

PyTorch 使用 Python 重设计和实现了 Torch，同时共享相同的核心 C 库作为后端代码。PyTorch 开发人员调整了这个后端代码以高效地运行 Python。他们还保留了基于 GPU 的硬件加速以及使基于 Lua 的 Torch 成为可能的扩展功能。

特性

PyTorch 的主要特性如下：

简单的接口 - PyTorch 提供易于使用的 API；因此它被认为非常易于操作，并且在 Python 上运行。在这个框架中的代码执行非常容易。

Python 使用 - 这个库被认为是 Pythonic 的，它与 Python 数据科学栈无缝集成。因此，它可以利用 Python 环境提供的所有服务和功能。

计算图 - PyTorch 提供了一个优秀的平台，它提供动态计算图。因此用户可以在运行时更改它们。当开发人员不知道创建神经网络模型需要多少内存时，这非常有用。

PyTorch 以具有以下三个抽象级别而闻名：

• 张量 - 在 GPU 上运行的命令式 n 维数组。

• 变量 - 计算图中的节点。它存储数据和梯度。

• 模块 - 神经网络层，它将存储状态或可学习的权重。

PyTorch 的优势

以下是 PyTorch 的优势：

• 易于调试和理解代码。

• 它包含许多与 Torch 相同的层。

• 它包含许多损失函数。

• 它可以被认为是 NumPy 对 GPU 的扩展。

• 它允许构建其结构依赖于计算本身的网络。

TensorFlow 与 PyTorch

我们将看看 TensorFlow 和 PyTorch 之间的主要区别：

PyTorch - 安装

PyTorch 是一个流行的深度学习框架。在本教程中，我们将“Windows 10”作为我们的操作系统。成功环境设置的步骤如下：

步骤 1

以下链接包含一个软件包列表，其中包含适用于 PyTorch 的合适的软件包。

https://drive.google.com/drive/folders/0B-X0-FlSGfCYdTNldW02UGl4MXM

您需要做的就是下载相应的软件包并按照以下屏幕截图所示安装它：

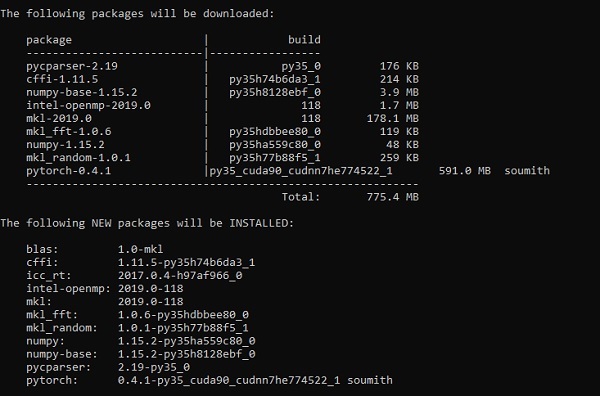
步骤 2

它涉及使用 Anaconda 框架验证 PyTorch 框架的安装。

使用以下命令验证：

conda list

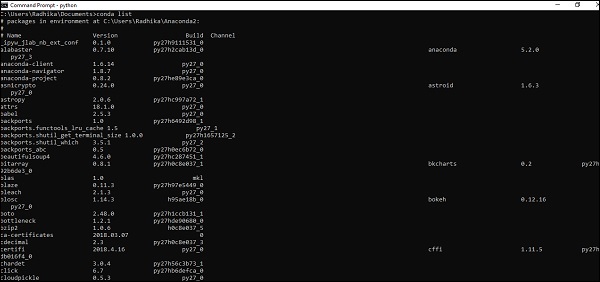
“Conda list” 显示已安装的框架列表。

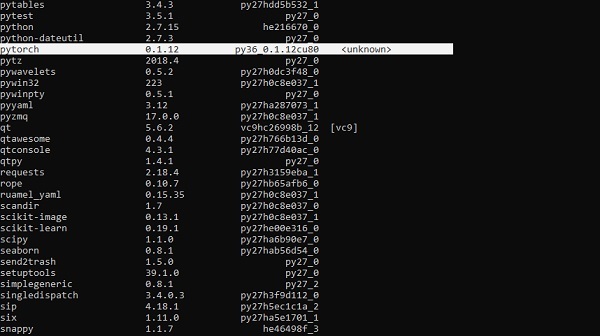
突出显示的部分表明 PyTorch 已成功安装到我们的系统中。

神经网络的数学基础

数学在任何机器学习算法中都至关重要，它包含各种核心数学概念，以设计出特定方式的正确算法。

以下是数学主题对机器学习和数据科学的重要性：

现在，让我们关注机器学习中重要的数学概念，这些概念对于自然语言处理来说很重要：

向量

向量被认为是数字数组，可以是连续的或离散的，包含向量的空间称为向量空间。向量的空间维度可以是有限的或无限的，但据观察，机器学习和数据科学问题处理的是固定长度的向量。

向量表示如下所示：

temp = torch.FloatTensor([23,24,24.5,26,27.2,23.0])
temp.size()
Output - torch.Size([6])

在机器学习中，我们处理多维数据。因此，向量变得非常重要，并被认为是任何预测问题陈述的输入特征。

标量

标量被定义为只有零维且只包含一个值的量。在 PyTorch 中，它不包含一个特殊的零维张量；因此，声明将如下进行：

x = torch.rand(10)
x.size()
Output - torch.Size([10])

矩阵

大多数结构化数据通常以表格或特定矩阵的形式表示。我们将使用一个名为波士顿房价的数据集，它在 Python scikit-learn 机器学习库中很容易获得。

boston_tensor = torch.from_numpy(boston.data)
boston_tensor.size()
Output: torch.Size([506, 13])
boston_tensor[:2]
Output:
Columns 0 to 7
0.0063 18.0000 2.3100 0.0000 0.5380 6.5750 65.2000 4.0900
0.0273 0.0000 7.0700 0.0000 0.4690 6.4210 78.9000 4.9671
Columns 8 to 12
1.0000 296.0000 15.3000 396.9000 4.9800
2.0000 242.0000 17.8000 396.9000 9.1400

PyTorch - 神经网络基础

神经网络的主要原理包括一系列基本元素，即人工神经元或感知器。它包括几个基本输入，例如 x1、x2……xn，如果总和大于激活电位，则产生二进制输出。

示例神经元的示意图如下所示：

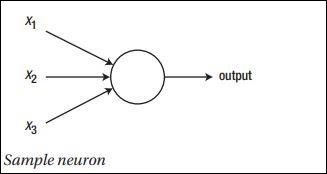
生成的输出可以被认为是带激活电位或偏差的加权和。

$$Output=\sum_jw_jx_j+Bias$$

典型的神经网络架构如下所示：

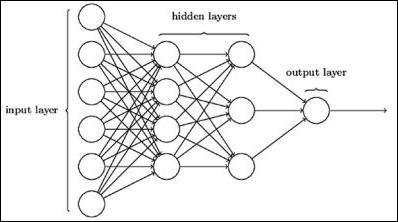
输入和输出之间的层称为隐藏层，层之间连接的密度和类型是配置。例如，全连接配置具有连接到 L+1 层的所有 L 层神经元。对于更明显的局部化，我们可以只连接局部邻域，例如九个神经元，到下一层。图 1-9 说明了具有密集连接的两个隐藏层。

各种类型的神经网络如下：

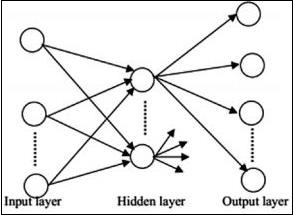
前馈神经网络

前馈神经网络包括神经网络家族的基本单元。这种类型的神经网络中的数据移动是从输入层到输出层，通过存在的隐藏层。一层的一个输出作为输入层，限制了网络架构中任何类型的循环。

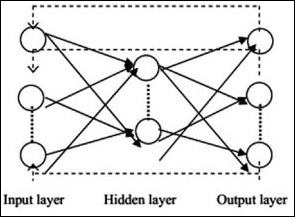
循环神经网络

当数据模式随时间连续变化时，就是循环神经网络。在 RNN 中，相同的层用于接受输入参数并在指定的神经网络中显示输出参数。

可以使用 torch.nn 包构建神经网络。

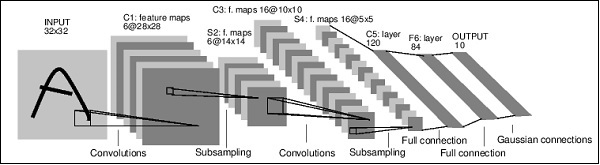
这是一个简单的前馈网络。它接收输入，将其依次馈送到多层，然后最终给出输出。

借助 PyTorch，我们可以使用以下步骤进行神经网络的典型训练过程：

• 定义具有某些可学习参数（或权重）的神经网络。
• 迭代输入数据集。
• 通过网络处理输入。
• 计算损失（输出与正确结果的距离）。
• 将梯度反向传播到网络的参数中。
• 更新网络的权重，通常使用如下所示的简单更新

rule: weight = weight -learning_rate * gradient

机器学习的通用工作流程

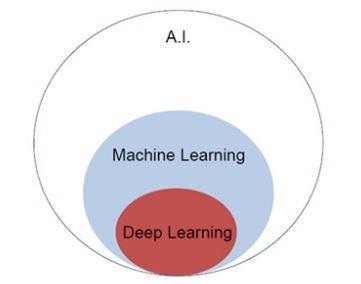
人工智能如今正日益流行。机器学习和深度学习构成了人工智能。下面的维恩图解释了机器学习和深度学习之间的关系。

机器学习

机器学习是一门允许计算机根据设计和编程的算法运行的科学艺术。许多研究人员认为机器学习是朝着人类水平人工智能取得进展的最佳途径。它包括各种类型的模式，例如：

• 监督学习模式
• 无监督学习模式

深度学习

深度学习是机器学习的一个子领域，其中所关注的算法的灵感来自大脑的结构和功能，称为人工神经网络。

深度学习通过监督学习或从标记数据和算法中学习而获得了极大的重视。深度学习中的每个算法都经历相同的过程。它包括输入的分层非线性变换，并用于创建统计模型作为输出。

机器学习过程使用以下步骤定义：

• 识别相关数据集并为分析准备它们。
• 选择要使用的算法类型。
• 基于所使用的算法构建分析模型。
• 在测试数据集上训练模型，根据需要进行修改。
• 运行模型以生成测试分数。

PyTorch - 机器学习与深度学习

在本章中，我们将讨论机器学习和深度学习概念之间的主要区别。

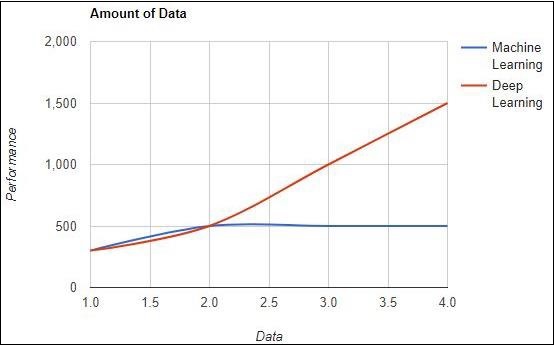
数据量

机器学习使用不同数量的数据，主要用于少量数据。另一方面，深度学习如果数据量迅速增加，则可以高效地工作。下图描述了机器学习和深度学习关于数据量的运行情况：

硬件依赖性

深度学习算法的设计严重依赖于高端机器，这与传统的机器学习算法相反。深度学习算法执行大量的矩阵乘法运算，这需要巨大的硬件支持。

特征工程

特征工程是将领域知识放入特定特征以降低数据复杂性并使学习算法可见的模式的过程。

例如，传统的机器学习模式侧重于像素和其他特征工程过程所需的属性。深度学习算法侧重于来自数据的高级特征。它减少了为每个新问题开发新的特征提取器的任务。

PyTorch - 实现第一个神经网络

PyTorch 包含创建和实现神经网络的特殊功能。在本章中，我们将创建一个具有一个隐藏层并开发单个输出单元的简单神经网络。

我们将使用以下步骤来使用 PyTorch 实现第一个神经网络：

步骤 1

首先，我们需要使用以下命令导入 PyTorch 库：

import torch 
import torch.nn as nn

步骤 2

定义所有层和批次大小以开始执行神经网络，如下所示：

# Defining input size, hidden layer size, output size and batch size respectively
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

步骤 3

由于神经网络包括输入数据的组合以获得相应的输出数据，我们将遵循以下相同步骤：

# Create dummy input and target tensors (data)
x = torch.randn(batch_size, n_in)
y = torch.tensor([[1.0], [0.0], [0.0], 
[1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])

步骤 4

使用内置函数创建一个顺序模型。使用下面的代码行创建一个顺序模型：

# Create a model
model = nn.Sequential(nn.Linear(n_in, n_h),
   nn.ReLU(),
   nn.Linear(n_h, n_out),
   nn.Sigmoid())

步骤 5

使用梯度下降优化器构建损失函数，如下所示：

Construct the loss function
criterion = torch.nn.MSELoss()
# Construct the optimizer (Stochastic Gradient Descent in this case)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

步骤 6

使用给定的代码行实现带有迭代循环的梯度下降模型：

# Gradient Descent
for epoch in range(50):
   # Forward pass: Compute predicted y by passing x to the model
   y_pred = model(x)

   # Compute and print loss
   loss = criterion(y_pred, y)
   print('epoch: ', epoch,' loss: ', loss.item())

   # Zero gradients, perform a backward pass, and update the weights.
   optimizer.zero_grad()

   # perform a backward pass (backpropagation)
   loss.backward()

   # Update the parameters
   optimizer.step()

步骤 7

生成的输出如下：

epoch: 0 loss: 0.2545787990093231
epoch: 1 loss: 0.2545052170753479
epoch: 2 loss: 0.254431813955307
epoch: 3 loss: 0.25435858964920044
epoch: 4 loss: 0.2542854845523834
epoch: 5 loss: 0.25421255826950073
epoch: 6 loss: 0.25413978099823
epoch: 7 loss: 0.25406715273857117
epoch: 8 loss: 0.2539947032928467
epoch: 9 loss: 0.25392240285873413
epoch: 10 loss: 0.25385022163391113
epoch: 11 loss: 0.25377824902534485
epoch: 12 loss: 0.2537063956260681
epoch: 13 loss: 0.2536346912384033
epoch: 14 loss: 0.25356316566467285
epoch: 15 loss: 0.25349172949790955
epoch: 16 loss: 0.25342053174972534
epoch: 17 loss: 0.2533493936061859
epoch: 18 loss: 0.2532784342765808
epoch: 19 loss: 0.25320762395858765
epoch: 20 loss: 0.2531369626522064
epoch: 21 loss: 0.25306645035743713
epoch: 22 loss: 0.252996027469635
epoch: 23 loss: 0.2529257833957672
epoch: 24 loss: 0.25285571813583374
epoch: 25 loss: 0.25278574228286743
epoch: 26 loss: 0.25271597504615784
epoch: 27 loss: 0.25264623761177063
epoch: 28 loss: 0.25257670879364014
epoch: 29 loss: 0.2525072991847992
epoch: 30 loss: 0.2524380087852478
epoch: 31 loss: 0.2523689270019531
epoch: 32 loss: 0.25229987502098083
epoch: 33 loss: 0.25223103165626526
epoch: 34 loss: 0.25216227769851685
epoch: 35 loss: 0.252093642950058
epoch: 36 loss: 0.25202515721321106
epoch: 37 loss: 0.2519568204879761
epoch: 38 loss: 0.251888632774353
epoch: 39 loss: 0.25182053446769714
epoch: 40 loss: 0.2517525553703308
epoch: 41 loss: 0.2516847252845764
epoch: 42 loss: 0.2516169846057892
epoch: 43 loss: 0.2515493929386139
epoch: 44 loss: 0.25148195028305054
epoch: 45 loss: 0.25141456723213196
epoch: 46 loss: 0.2513473629951477
epoch: 47 loss: 0.2512802183628082
epoch: 48 loss: 0.2512132525444031
epoch: 49 loss: 0.2511464059352875

PyTorch - 神经网络到功能块

训练深度学习算法包括以下步骤：

• 构建数据管道
• 构建网络架构
• 使用损失函数评估架构
• 使用优化算法优化网络架构权重

训练特定的深度学习算法正是将神经网络转换为功能块的具体要求，如下所示：

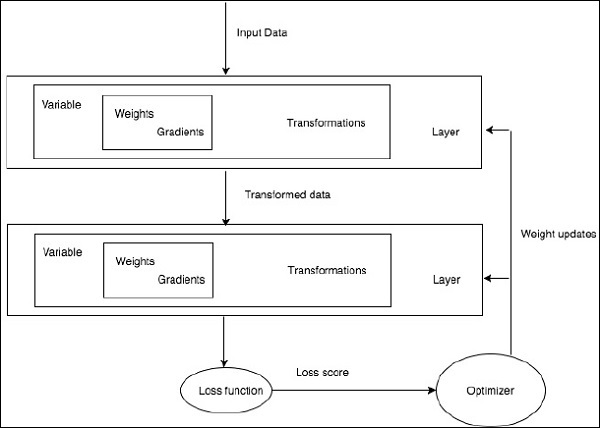
根据上图，任何深度学习算法都涉及获取输入数据，构建相应的架构，其中包含嵌入其中的许多层。

如果您观察上图，则使用损失函数根据神经网络权重的优化来评估准确性。

PyTorch - 术语

在本章中，我们将讨论 PyTorch 中一些最常用的术语。

PyTorch NumPy

PyTorch 张量与 NumPy 数组相同。张量是 n 维数组，对于 PyTorch 而言，它提供了许多用于操作这些张量的函数。

PyTorch 张量通常利用 GPU 来加速其数值计算。这些在 PyTorch 中创建的张量可用于将两层网络拟合到随机数据。用户可以手动实现网络的正向和反向传递。

变量和自动梯度

使用 autograd 时，网络的正向传递将定义一个计算图 - 图中的节点将是张量，边将是根据输入张量生成输出张量的函数。

PyTorch 张量可以创建为变量对象，其中变量表示计算图中的节点。

动态图

静态图很好，因为用户可以预先优化图。如果程序员反复重用相同的图，那么这种潜在的代价高昂的预先优化可以保持不变，因为相同的图会被反复运行。

它们的主要区别在于 TensorFlow 的计算图是静态的，而 PyTorch 使用动态计算图。

Optim 包

PyTorch 中的 optim 包抽象了以多种方式实现的优化算法的概念，并提供了常用优化算法的示例。这可以在 import 语句中调用。

多进程

多进程支持相同的操作，以便所有张量都在多个处理器上工作。队列将把它们的数据移入共享内存，并且只会向另一个进程发送句柄。

PyTorch - 加载数据

PyTorch 包含一个名为 torchvision 的包，用于加载和准备数据集。它包括两个基本函数，即 Dataset 和 DataLoader，它们有助于数据集的转换和加载。

数据集

Dataset 用于从给定数据集中读取和转换数据点。实现的基本语法如下所示：

trainset = torchvision.datasets.CIFAR10(root = './data', train = True,
   download = True, transform = transform)

DataLoader 用于打乱和批量处理数据。它可以用来使用多进程工作程序并行加载数据。

trainloader = torch.utils.data.DataLoader(trainset, batch_size = 4,
   shuffle = True, num_workers = 2)

示例：加载 CSV 文件

我们使用 Python 包 Panda 来加载 csv 文件。原始文件具有以下格式：（图像名称，68 个地标 - 每个地标都有 x，y 坐标）。

landmarks_frame = pd.read_csv('faces/face_landmarks.csv')

n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1, 2)

PyTorch - 线性回归

在本章中，我们将重点介绍使用 TensorFlow 实现线性回归的基本示例。逻辑回归或线性回归是一种监督机器学习方法，用于对有序离散类别进行分类。本章的目标是构建一个模型，用户可以通过该模型预测预测变量和一个或多个自变量之间的关系。

这两个变量之间的关系被认为是线性的，即，如果 y 是因变量，x 被认为是自变量，那么这两个变量的线性回归关系将如下所示：

Y = Ax+b

接下来，我们将设计一个线性回归算法，使我们能够理解下面给出的两个重要概念：

• 成本函数
• 梯度下降算法

线性回归的示意图如下所示

解释结果

$$Y=ax+b$$

• a 的值是斜率。

• b 的值是y 截距。

• r 是相关系数。

• r² 是相关系数。

线性回归方程的图形视图如下所示：

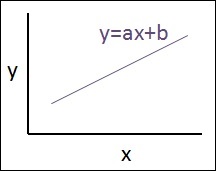
使用 PyTorch 实现线性回归使用以下步骤：

步骤 1

使用以下代码导入创建 PyTorch 中的线性回归所需的包：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

步骤 2

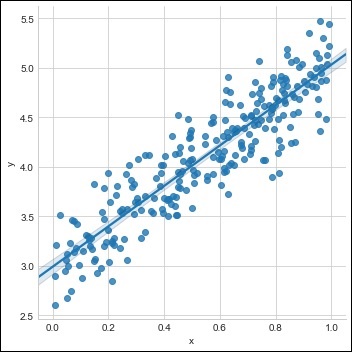
使用可用的数据集创建一个单一的训练集，如下所示：

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)

步骤 3

使用下面提到的 PyTorch 库实现线性回归：

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
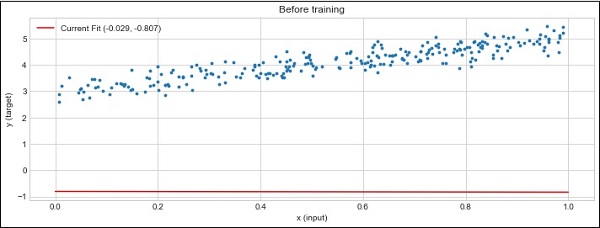
plot_current_fit('Before training')

生成的绘图如下所示：

PyTorch - 卷积神经网络

深度学习是机器学习的一个分支，被认为是近几十年来研究人员采取的关键步骤。深度学习实现的例子包括图像识别和语音识别等应用。

下面给出两种重要的深度神经网络类型：

• 卷积神经网络
• 循环神经网络。

在本章中，我们将重点介绍第一种类型，即卷积神经网络 (CNN)。

卷积神经网络

卷积神经网络旨在通过多层数组处理数据。这种类型的神经网络用于图像识别或人脸识别等应用。

CNN 与任何其他普通神经网络的主要区别在于，CNN 将输入作为二维数组，并直接对图像进行操作，而不是关注其他神经网络关注的特征提取。

CNN 的主要方法包括解决识别问题。谷歌和 Facebook 等顶级公司已投资识别项目的研发项目，以更快地完成活动。

每个卷积神经网络都包含三个基本思想：

• 局部感受野
• 卷积
• 池化

让我们详细了解这些术语。

局部感受野

CNN 利用输入数据中存在的空间相关性。神经网络的并发层中的每一个都连接一些输入神经元。这个特定区域称为局部感受野。它只关注隐藏神经元。隐藏神经元将处理所述字段内的输入数据，而不会意识到特定边界之外的变化。

生成局部感受野的图表表示如下：

卷积

在上图中，我们观察到每个连接学习隐藏神经元与从一层移动到另一层的相关连接的权重。在这里，单个神经元会不时进行移位。此过程称为“卷积”。

从输入层到隐藏特征图的连接映射定义为“共享权重”，包含的偏差称为“共享偏差”。

池化

卷积神经网络使用池化层，这些层位于 CNN 声明之后。它将用户的输入作为从卷积网络输出的特征图，并准备一个压缩的特征图。池化层有助于创建具有前一层神经元的层。

PyTorch 的实现

使用以下步骤创建使用 PyTorch 的卷积神经网络。

步骤 1

导入创建简单神经网络所需的包。

from torch.autograd import Variable
import torch.nn.functional as F

步骤 2

创建一个具有卷积神经网络批量表示的类。我们的输入 x 批次形状的维度为 (3, 32, 32)。

class SimpleCNN(torch.nn.Module):
   def __init__(self):
      super(SimpleCNN, self).__init__()
      #Input channels = 3, output channels = 18
      self.conv1 = torch.nn.Conv2d(3, 18, kernel_size = 3, stride = 1, padding = 1)
      self.pool = torch.nn.MaxPool2d(kernel_size = 2, stride = 2, padding = 0)
      #4608 input features, 64 output features (see sizing flow below)
      self.fc1 = torch.nn.Linear(18 * 16 * 16, 64)
      #64 input features, 10 output features for our 10 defined classes
      self.fc2 = torch.nn.Linear(64, 10)

步骤 3

计算第一个卷积的激活大小，从 (3, 32, 32) 变为 (18, 32, 32)。

维度大小从 (18, 32, 32) 变为 (18, 16, 16)。由于神经网络输入层的维度重塑，大小从 (18, 16, 16) 变为 (1, 4608)。

回想一下，-1 从其他给定的维度推断出这个维度。

def forward(self, x):
   x = F.relu(self.conv1(x))
   x = self.pool(x)
   x = x.view(-1, 18 * 16 *16)
   x = F.relu(self.fc1(x))
   #Computes the second fully connected layer (activation applied later)
   #Size changes from (1, 64) to (1, 10)
   x = self.fc2(x)
   return(x)

PyTorch - 循环神经网络

循环神经网络是一种面向深度学习的算法，它采用顺序方法。在神经网络中，我们总是假设每个输入和输出都独立于所有其他层。这些类型的神经网络被称为循环神经网络，因为它们以顺序方式执行数学计算，一个接一个地完成任务。

下图指定了循环神经网络的完整方法和工作原理：

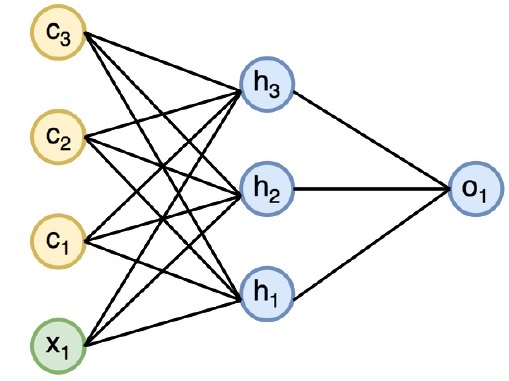
在上图中，c1、c2、c3 和 x1 被认为是输入，其中包括一些隐藏输入值，即 h1、h2 和 h3，它们提供相应的输出 o1。我们现在将重点介绍使用 PyTorch 来创建正弦波。

在训练期间，我们将对我们的模型采用一次一个数据点的训练方法。输入序列 x 包含 20 个数据点，目标序列被认为与输入序列相同。

步骤 1

使用以下代码导入实现循环神经网络所需的包：

import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as init

步骤 2

我们将设置模型超参数，输入层的大小设置为 7。将有 6 个上下文神经元和 1 个输入神经元来创建目标序列。

dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))

x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)

我们将生成训练数据，其中 x 是输入数据序列，y 是所需的目标序列。

步骤 3

循环神经网络中的权重使用具有零均值的正态分布进行初始化。W1 将表示接受输入变量，w2 将表示生成的输出，如下所示：

w1 = torch.FloatTensor(input_size, 
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)

步骤 4

现在，重要的是为前馈创建唯一定义神经网络的函数。

def forward(input, context_state, w1, w2):
   xh = torch.cat((input, context_state), 1)
   context_state = torch.tanh(xh.mm(w1))
   out = context_state.mm(w2)
   return (out, context_state)

步骤 5

下一步是开始循环神经网络的正弦波实现的训练过程。外循环迭代每个循环，内循环迭代序列的元素。在这里，我们还将计算均方误差 (MSE)，这有助于预测连续变量。

for i in range(epochs):
   total_loss = 0
   context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
   for j in range(x.size(0)):
      input = x[j:(j+1)]
      target = y[j:(j+1)]
      (pred, context_state) = forward(input, context_state, w1, w2)
      loss = (pred - target).pow(2).sum()/2
      total_loss += loss
      loss.backward()
      w1.data -= lr * w1.grad.data
      w2.data -= lr * w2.grad.data
      w1.grad.data.zero_()
      w2.grad.data.zero_()
      context_state = Variable(context_state.data)
   if i % 10 == 0:
      print("Epoch: {} loss {}".format(i, total_loss.data[0]))

context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []

for i in range(x.size(0)):
   input = x[i:i+1]
   (pred, context_state) = forward(input, context_state, w1, w2)
   context_state = context_state
   predictions.append(pred.data.numpy().ravel()[0])

步骤 6

现在，是时候绘制正弦波了。

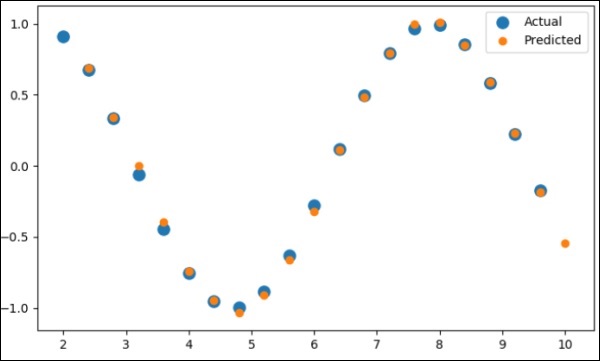
pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()

输出

上述过程的输出如下：

PyTorch - 数据集

在本章中，我们将更多地关注torchvision.datasets及其各种类型。PyTorch 包含以下数据集加载器：

• MNIST
• COCO（图像标题生成和目标检测）

数据集主要包含以下两种类型的函数：

• Transform − 一个函数，它接收图像作为输入，并返回一个修改后的标准化版本。这些变换函数可以组合在一起。

• Target_transform − 一个函数，它接收目标并对其进行变换。例如，接收标题字符串作为输入，并返回一个单词索引张量。

MNIST

以下是MNIST数据集的示例代码：

dset.MNIST(root, train = TRUE, transform = NONE, 
target_transform = None, download = FALSE)

参数如下：

• root − 数据集的根目录，其中包含已处理的数据。

• train − True = 训练集，False = 测试集

• download − True = 从互联网下载数据集并将其放入根目录。

COCO

这需要安装COCO API。以下示例演示了使用PyTorch实现COCO数据集：

import torchvision.dataset as dset
import torchvision.transforms as transforms
cap = dset.CocoCaptions(root = ‘ dir where images are’, 
annFile = ’json annotation file’,
transform = transforms.ToTensor())
print(‘Number of samples: ‘, len(cap))
print(target)

取得的输出如下：

Number of samples: 82783
Image Size: (3L, 427L, 640L)

PyTorch - 卷积神经网络简介

卷积神经网络（Convnets）是关于从零开始构建CNN模型的。网络架构将包含以下步骤的组合：

• Conv2d (二维卷积)
• MaxPool2d (最大池化)
• 修正线性单元 (ReLU)
• View (视图变换)
• 线性层

模型训练

模型训练过程与图像分类问题相同。以下代码片段完成了在提供的数据集上训练模型的过程：

def fit(epoch,model,data_loader,phase 
= 'training',volatile = False):
   if phase == 'training':
      model.train()
   if phase == 'training':
      model.train()
   if phase == 'validation':
      model.eval()
   volatile=True
   running_loss = 0.0
   running_correct = 0
   for batch_idx , (data,target) in enumerate(data_loader):
      if is_cuda:
         data,target = data.cuda(),target.cuda()
         data , target = Variable(data,volatile),Variable(target)
      if phase == 'training':
         optimizer.zero_grad()
         output = model(data)
         loss = F.nll_loss(output,target)
         running_loss + = 
         F.nll_loss(output,target,size_average = 
         False).data[0]
         preds = output.data.max(dim = 1,keepdim = True)[1]
         running_correct + = 
         preds.eq(target.data.view_as(preds)).cpu().sum()
         if phase == 'training':
            loss.backward()
            optimizer.step()
   loss = running_loss/len(data_loader.dataset)
   accuracy = 100. * running_correct/len(data_loader.dataset)
   print(f'{phase} loss is {loss:{5}.{2}} and {phase} accuracy is {running_correct}/{len(data_loader.dataset)}{accuracy:{return loss,accuracy}})

该方法包含用于训练和验证的不同逻辑。使用不同模式有两个主要原因：

• 在训练模式下，dropout会移除一定比例的值，这在验证或测试阶段不应该发生。

• 在训练模式下，我们计算梯度并更改模型的参数值，但在测试或验证阶段不需要反向传播。

PyTorch - 从零开始训练卷积神经网络

在本章中，我们将重点介绍从零开始创建卷积神经网络。这意味着使用torch创建相应的卷积神经网络或示例神经网络。

步骤 1

创建一个具有相应参数的必要类。参数包括具有随机值的权重。

class Neural_Network(nn.Module):
   def __init__(self, ):
      super(Neural_Network, self).__init__()
      self.inputSize = 2
      self.outputSize = 1
      self.hiddenSize = 3
      # weights
      self.W1 = torch.randn(self.inputSize, 
      self.hiddenSize) # 3 X 2 tensor
      self.W2 = torch.randn(self.hiddenSize, self.outputSize) # 3 X 1 tensor

步骤 2

创建一个具有sigmoid函数的前馈模式函数。

def forward(self, X):
   self.z = torch.matmul(X, self.W1) # 3 X 3 ".dot" 
   does not broadcast in PyTorch
   self.z2 = self.sigmoid(self.z) # activation function
   self.z3 = torch.matmul(self.z2, self.W2)
   o = self.sigmoid(self.z3) # final activation 
   function
   return o
   def sigmoid(self, s):
      return 1 / (1 + torch.exp(-s))
   def sigmoidPrime(self, s):
      # derivative of sigmoid
      return s * (1 - s)
   def backward(self, X, y, o):
      self.o_error = y - o # error in output
      self.o_delta = self.o_error * self.sigmoidPrime(o) # derivative of sig to error
      self.z2_error = torch.matmul(self.o_delta, torch.t(self.W2))
      self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2)
      self.W1 + = torch.matmul(torch.t(X), self.z2_delta)
      self.W2 + = torch.matmul(torch.t(self.z2), self.o_delta)

步骤 3

创建如下所示的训练和预测模型：

def train(self, X, y):
   # forward + backward pass for training
   o = self.forward(X)
   self.backward(X, y, o)
def saveWeights(self, model):
   # Implement PyTorch internal storage functions
   torch.save(model, "NN")
   # you can reload model with all the weights and so forth with:
   # torch.load("NN")
def predict(self):
   print ("Predicted data based on trained weights: ")
   print ("Input (scaled): \n" + str(xPredicted))
   print ("Output: \n" + str(self.forward(xPredicted)))

PyTorch - 卷积神经网络中的特征提取

卷积神经网络包含一个主要特征：特征提取。使用以下步骤实现卷积神经网络的特征提取。

步骤 1

导入相应的模型，使用“PyTorch”创建特征提取模型。

import torch
import torch.nn as nn
from torchvision import models

步骤 2

创建一个特征提取器类，可以在需要时调用。

class Feature_extractor(nn.module):
   def forward(self, input):
      self.feature = input.clone()
      return input
new_net = nn.Sequential().cuda() # the new network
target_layers = [conv_1, conv_2, conv_4] # layers you want to extract`
i = 1
for layer in list(cnn):
   if isinstance(layer,nn.Conv2d):
      name = "conv_"+str(i)
      art_net.add_module(name,layer)
      if name in target_layers:
         new_net.add_module("extractor_"+str(i),Feature_extractor())
      i+=1
   if isinstance(layer,nn.ReLU):
      name = "relu_"+str(i)
      new_net.add_module(name,layer)
   if isinstance(layer,nn.MaxPool2d):
      name = "pool_"+str(i)
      new_net.add_module(name,layer)
new_net.forward(your_image)
print (new_net.extractor_3.feature)

PyTorch - 卷积神经网络的可视化

在本章中，我们将重点介绍借助卷积神经网络进行数据可视化模型。要获得卷积神经网络可视化的完美图像，需要执行以下步骤。

步骤 1

导入对卷积神经网络可视化很重要的必要模块。

import os
import numpy as np
import pandas as pd
from scipy.misc import imread
from sklearn.metrics import accuracy_score

import keras
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Flatten, Activation, Input
from keras.layers import Conv2D, MaxPooling2D
import torch

步骤 2

为了避免训练和测试数据中的潜在随机性，请调用如下代码中给出的相应数据集：

seed = 128
rng = np.random.RandomState(seed)
data_dir = "../../datasets/MNIST"
train = pd.read_csv('../../datasets/MNIST/train.csv')
test = pd.read_csv('../../datasets/MNIST/Test_fCbTej3.csv')
img_name = rng.choice(train.filename)
filepath = os.path.join(data_dir, 'train', img_name)
img = imread(filepath, flatten=True)

步骤 3

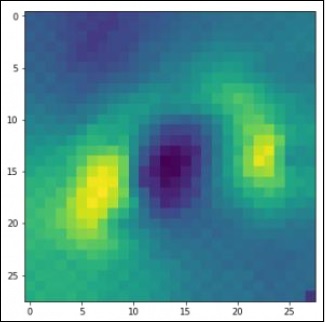
使用以下代码绘制必要的图像，以完美的方式定义训练和测试数据：

pylab.imshow(img, cmap ='gray')
pylab.axis('off')
pylab.show()

输出如下所示：

PyTorch - 使用卷积神经网络进行序列处理

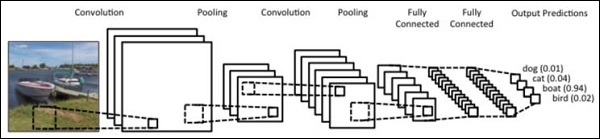
在本章中，我们提出了一种替代方法，它依赖于在两个序列上使用单个二维卷积神经网络。我们网络的每一层都基于迄今为止生成的输出序列重新编码源标记。因此，注意力特性在整个网络中普遍存在。

在这里，我们将重点介绍创建具有特定池化的顺序网络，这些池化来自数据集中包含的值。此过程也最适用于“图像识别模块”。

使用以下步骤使用PyTorch创建使用卷积神经网络的序列处理模型：

步骤 1

导入使用卷积神经网络进行序列处理所需的模块。

import keras 
from keras.datasets import mnist 
from keras.models import Sequential 
from keras.layers import Dense, Dropout, Flatten 
from keras.layers import Conv2D, MaxPooling2D 
import numpy as np

步骤 2

执行必要的操作，使用以下代码在相应序列中创建模式：

batch_size = 128 
num_classes = 10 
epochs = 12
# input image dimensions 
img_rows, img_cols = 28, 28
# the data, split between train and test sets 
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000,28,28,1) 
x_test = x_test.reshape(10000,28,28,1)
print('x_train shape:', x_train.shape) 
print(x_train.shape[0], 'train samples') 
print(x_test.shape[0], 'test samples')
y_train = keras.utils.to_categorical(y_train, num_classes) 
y_test = keras.utils.to_categorical(y_test, num_classes)

步骤 3

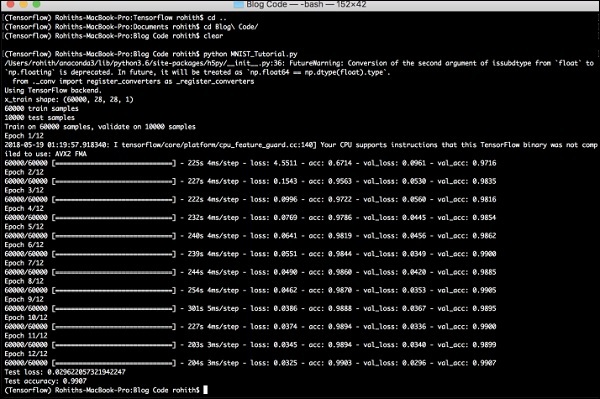
编译模型并将模式拟合到提到的卷积神经网络模型中，如下所示：

model.compile(loss = 
keras.losses.categorical_crossentropy, 
optimizer = keras.optimizers.Adadelta(), metrics = 
['accuracy'])
model.fit(x_train, y_train, 
batch_size = batch_size, epochs = epochs, 
verbose = 1, validation_data = (x_test, y_test)) 
score = model.evaluate(x_test, y_test, verbose = 0) 
print('Test loss:', score[0]) 
print('Test accuracy:', score[1])

生成的输出如下：

PyTorch - 词嵌入

在本章中，我们将了解著名的词嵌入模型——word2vec。word2vec模型用于借助一组相关模型生成词嵌入。word2vec模型使用纯C代码实现，梯度是手动计算的。

在PyTorch中实现word2vec模型的步骤如下：

步骤 1

如下所示实现词嵌入中的库：

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

步骤 2

使用名为word2vec的类实现词嵌入的Skip Gram模型。它包括emb_size、emb_dimension、u_embedding、v_embedding类型的属性。

class SkipGramModel(nn.Module):
   def __init__(self, emb_size, emb_dimension):
      super(SkipGramModel, self).__init__()
      self.emb_size = emb_size
      self.emb_dimension = emb_dimension
      self.u_embeddings = nn.Embedding(emb_size, emb_dimension, sparse=True)
      self.v_embeddings = nn.Embedding(emb_size, emb_dimension, sparse = True)
      self.init_emb()
   def init_emb(self):
      initrange = 0.5 / self.emb_dimension
      self.u_embeddings.weight.data.uniform_(-initrange, initrange)
      self.v_embeddings.weight.data.uniform_(-0, 0)
   def forward(self, pos_u, pos_v, neg_v):
      emb_u = self.u_embeddings(pos_u)
      emb_v = self.v_embeddings(pos_v)
      score = torch.mul(emb_u, emb_v).squeeze()
      score = torch.sum(score, dim = 1)
      score = F.logsigmoid(score)
      neg_emb_v = self.v_embeddings(neg_v)
      neg_score = torch.bmm(neg_emb_v, emb_u.unsqueeze(2)).squeeze()
      neg_score = F.logsigmoid(-1 * neg_score)
      return -1 * (torch.sum(score)+torch.sum(neg_score))
   def save_embedding(self, id2word, file_name, use_cuda):
      if use_cuda:
         embedding = self.u_embeddings.weight.cpu().data.numpy()
      else:
         embedding = self.u_embeddings.weight.data.numpy()
      fout = open(file_name, 'w')
      fout.write('%d %d\n' % (len(id2word), self.emb_dimension))
      for wid, w in id2word.items():
         e = embedding[wid]
         e = ' '.join(map(lambda x: str(x), e))
         fout.write('%s %s\n' % (w, e))
def test():
   model = SkipGramModel(100, 100)
   id2word = dict()
   for i in range(100):
      id2word[i] = str(i)
   model.save_embedding(id2word)         

步骤 3

实现主方法以正确显示词嵌入模型。

if __name__  ==  '__main__':
   test()

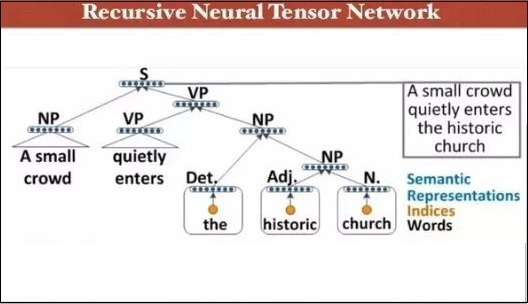
PyTorch - 递归神经网络

深度神经网络具有独有的功能，可以促进机器学习的突破，从而理解自然语言处理的过程。据观察，大多数这些模型将语言视为单词或字符的扁平序列，并使用一种称为循环神经网络或RNN的模型。

许多研究人员得出结论，最好根据短语的分层树来理解语言。这种类型包含在递归神经网络中，它考虑了特定的结构。

PyTorch具有一项特定功能，可以使这些复杂的自然语言处理模型变得更容易。它是一个功能齐全的深度学习框架，对计算机视觉有强大的支持。

递归神经网络的特性

• 递归神经网络的创建方式是：它包括对具有不同图状结构的相同权重集进行应用。

• 以拓扑顺序遍历节点。

• 这种类型的网络通过反向模式自动微分进行训练。

• 自然语言处理包含递归神经网络的一个特例。

• 这个递归神经张量网络在树中包含各种组合函数节点。

递归神经网络的示例如下所示：