数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时装研究
法律研究C++ 中的自我交叉
假设我们有一个包含 n 个数字的数组 x。我们从点 (0,0) 开始，向北移动 x[0] 个单位，然后向西移动 x[1] 个单位，向南移动 x[2] 个单位，向东移动 x[3] 个单位，依此类推。换句话说，每次移动后我们的方向都会逆时针改变。我们必须设计一个具有 O(1) 额外空间的一遍扫描算法来确定我们的路径是否自交叉。
因此，如果数组如下 − [3,4,2,5]
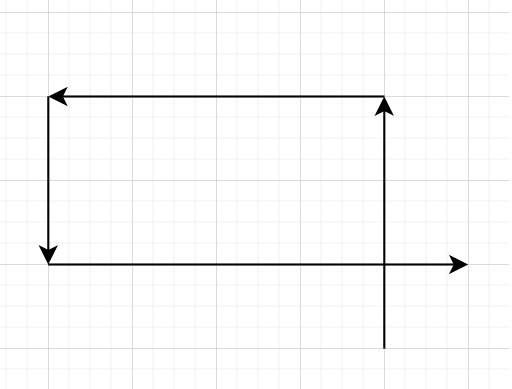
答案将为 true。
要解决这个问题，我们将按照以下步骤操作 −
在 x 的索引 4 处插入 0
n := x 的大小，i := 4
对于 i < n 且 x[i] > x[i - 2]，将 i 加 1，不初始化任何内容，执行 −
什么都不做
如果 i 等于 n，则返回 false
如果 x[i] >= x[i - 2] - x[i - 4]，则，
x[i - 1] = x[i - 1] - x[i - 3]
对于 i < n 且 x[i] < x[i - 2]，将 i 加 1，执行 −
什么都不做
当 i 不等于 n 时，返回 true
示例
让我们看下面的实现，以获得更好的理解 −
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool isSelfCrossing(vector<int>& x) {
x.insert(x.begin(), 4, 0);
int n = x.size();
int i = 4;
for(; i < n && x[i] > x[ i - 2];i++);
if(i == n) return false;
if (x[i] >= x[i - 2] - x[i - 4]){
x[i - 1] -= x[i - 3];
}
for (i++; i < n && x[i] < x[i - 2]; i++);
return i != n;
}
};
main(){
Solution ob;
vector<int> v = {3,4,2,5};
cout << (ob.isSelfCrossing(v));
}输入
{3,4,2,5}输出
1
更新时间：27-5-2020
207 次浏览
广告