单缝衍射

---

简介

波绕过障碍物的现象通常被称为衍射，基于这个简单的物理概念，本教程将解释单缝衍射的定义，同时解释衍射图案。此外，本教程还将包括对单缝衍射公式的解释以及对中心极大的定义。教程中将包含单缝衍射的计算。

什么是单缝衍射？

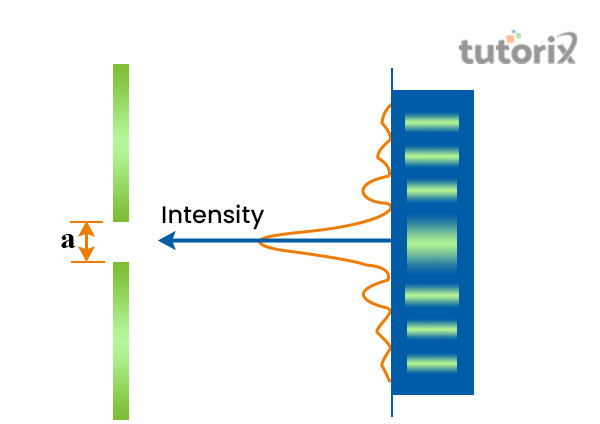
图 1：单缝衍射图案

光的弯曲现象通常在单缝衍射实验中观察到。实验证明，光波具有特定的波长，并且当光波在穿过狭缝时发生反应时，这些波长的频率可以发生变化（Qi & Wong，2022）。

在频率中观察到的这种变化通常会在放置在狭缝后面的屏幕上产生独特的图案，称为衍射图案。

单缝衍射：公式

单缝衍射的公式可以通过数学表示来表示。为了更好地理解，假设狭缝的宽度为

屏幕上任何一点的角度位置为 $\mathrm{\vartheta}$，其测量值是通过将狭缝的中心除以长度 a/2 得到的（Animations.physics.unsw，2022）。考虑到这一点，两条光线的辐射发生在彼此相距 a/2 的距离处。基于此，可以用数学方式表达的公式为

ΔL = a/2sinθ。

对于暗条纹，波长在 λ2 和 λ 之间计算。因此，第一条条纹的公式为 ΔL = λ2 = a/2sinθ，其中 λ = a sin θ，对于第二个极小值，公式为 λ/2 = a/4sin θ，其中 2λ = a sin θ。

中心极大值

中心极大值的位置在中心区域的宽度和极小值之间确定（Yin，He & Wu，2020）。基于这个概念，可以用简单的语言解释，中心极大值可以指从屏幕中心位置到一阶极小值的距离，该距离存在于中心的两个侧面。

在这种情况下，极小值的位置通常用 y 表示，其宽度通常从屏幕中心测量。这导致了公式的开发，即 tanθ $\approx$ θ$\approx$ y/D。基于此，对于小 ϑ，公式为 sin θ$\approx$θ。接下来，可以认为 i λ = a sin θ$\approx$aθ，这导致 θ = y/D = λa 或 y = λDa。现在专注于此以找到中心极大值的宽度，将认为宽度将表示为 2λDa，中心极大值的角宽度将为 2θ = 2λa。

单缝衍射：计算

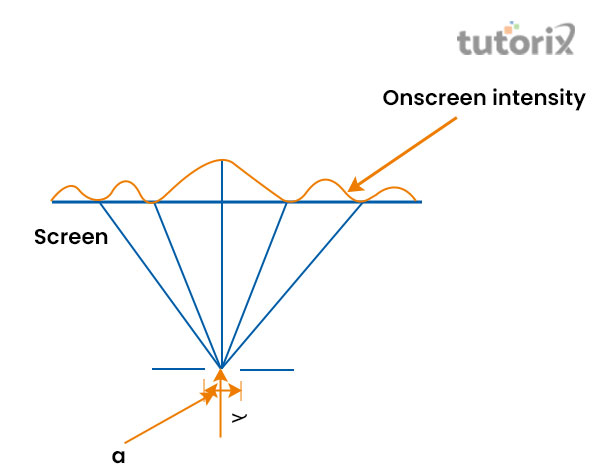
图 2：分析单缝衍射图案的图表

在图中可以看到狭缝很窄。这种情况被认为是一个常数，并且光与物体发生相互作用的事实必须与其波长的大小相当。它有助于展示光波的效果，例如单缝衍射的图案。由于宽度为 41°，因此中心极大值的扩展在原始光束中心位置的两侧为 20.7°。

通过单缝的衍射

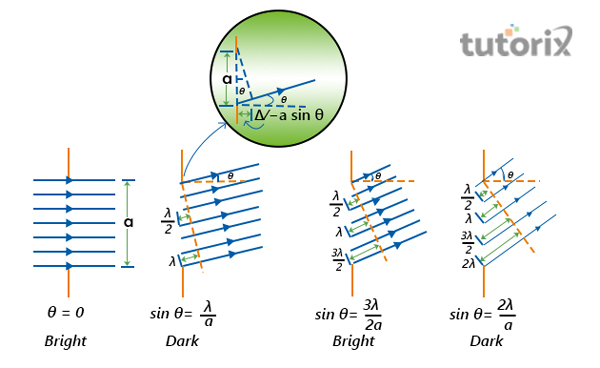
图 3：通过单缝的衍射

上图表示惠更斯原理的实验，该实验表明，如果光可以从不同方向聚焦到单缝上，则衍射将不同，或者光波的不同角波长（Phys.libretexts，2022）。在这个实验中，已经看到，大多数穿过狭缝的光线在穿过狭缝后具有另一条光线以建设性方式干涉，这导致在此角度处出现强度最大值。

结论

基于波的衍射概念，本教程解释了当光穿过一个单缝时可以观察到光的单缝衍射。这具有与光波长相当的宽度。在这种情况下，已经观察到极大值通常位于中心区域的宽度和极小值之间。

此外，本教程还表示了单缝衍射的公式，该公式表示为数学表示，ΔL = a/2sinθ。

常见问题

Q1. 衍射极小值和极大值是什么意思？

答：衍射极大值被认为是中心亮条纹，通常称为中心极大值，周围环绕着亮暗线。周围的暗亮线称为次级极小值。

Q2. 为什么光在单缝中发生衍射？

答：当光波穿过宽度与波长相似的狭缝时，穿过狭缝的光的一部分充当点光源，负责产生球面波。这是光发生衍射的主要原因。

Q3. 光的波长是多少？

答：当光波穿过特定相位时，波峰在波的路径中传播时会发生变化。这两个波峰之间的距离通常称为波长。

Q4. 单缝衍射和双缝衍射之间的核心区别是什么？

答：在单缝衍射的情况下，已经观察到极大值小于中心极大值，而穿过双缝时，它会产生均匀间隔的线，这些线在中心的两侧缓慢变暗。