静电感应电动势和动态感应电动势

感应电动势

当穿过导体或线圈的磁通量发生变化时，导体或线圈中就会感应出电动势，这被称为感应电动势。根据改变磁通量的方式，感应电动势分为两种：

• 静电感应电动势
• 动态感应电动势

静电感应电动势

当导体静止而磁场变化时，以这种方式感应的电动势称为静电感应电动势（如在变压器中）。之所以这样称呼，是因为电动势是在静止的导体中感应的。静电感应电动势还可以分为两类：

• 静电感应电动势
• 互感电动势

自感电动势

当由于线圈自身与其相关的磁通量变化而在线圈中感应出电动势时，这被称为自感电动势。

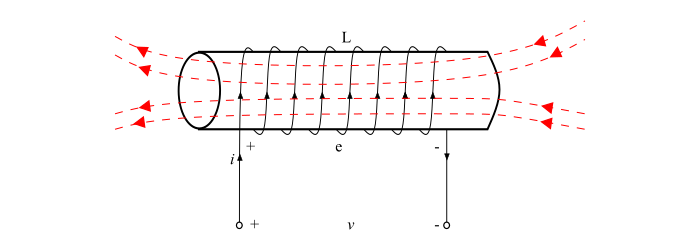
解释 - 当电流流过线圈时，由该电流产生的磁场穿过线圈。如果线圈中的电流发生变化，则与线圈相关的磁场也会发生变化。因此，根据法拉第电磁感应定律，线圈中会感应出电动势。这种感应电动势称为自感电动势。

在数学上，自感电动势由下式给出：

$$\mathrm{e=L\frac{di}{dt}\:\:\:\:\:\:...(1)}$$

其中，L 是线圈的自感。

互感电动势

当由于相邻线圈的磁通量变化而在线圈中感应出电动势时，这被称为互感电动势。

解释 - 考虑两个彼此相邻放置的线圈线圈-1 和线圈-2（见图）。线圈-1产生的磁通量的一部分与线圈-2相连。这两种线圈1和2共有的磁通量称为互感磁通量 $(\varphi_{m})$。现在，如果线圈-1中的电流发生变化，则互感磁通量也会发生变化，从而在线圈中感应出电动势。线圈-2中感应的电动势称为互感电动势，因为它是由线圈-1产生的磁通量变化引起的。在数学上，互感电动势由下式给出：

$$\mathrm{e_{m}=M\frac{di_{1}}{dt}\:\:\:\:\:\:...(2)}$$

其中，M 是线圈之间的互感。

动态感应电动势

当导体在静止磁场中移动，使得与其相关的磁通量的大小发生变化时，由于导体受到变化的磁场作用，因此会在其中感应出电动势。以这种方式感应的电动势称为动态感应电动势（如在直流或交流发电机中）。之所以这样称呼，是因为电动势是在运动的（动态的）导体中感应的。

解释 - 考虑一根长度为l 米的导体，它以 v m/s 的速度垂直于磁通密度为 B Wb/m² 的均匀静止磁场运动。设导体在时间dt 秒内移动一小段距离dx。然后，

$$\mathrm{导体扫过的面积,\mathit{a = l \times dx}\: \:m^{2}}$$

$$\mathrm{\therefore 导体切割的磁通量,\mathit{dψ}= 磁通密度 \:\times\: 扫过的面积}$$

$$\mathrm{\Longrightarrow \mathit{dψ=B \:l\:dx}\: \:Wb}$$

现在，根据法拉第电磁感应定律，感应电动势将是：

$$\mathrm{\mathit{e=N\frac{dψ}{dt}=\frac{B\:l\:dx}{dt}\: (\because N}=1)}$$

$$\mathrm{\because \mathit{\frac{dx}{dt}}=速度 \mathit{V}}$$

$$\mathrm{\therefore \mathit{e=B\: l\:v}\: \:伏特\:\:\:\:\:\:...(3)}$$

公式 (3) 给出了导体垂直于磁场运动时的动态感应电动势。

如果导体与磁场成θ角运动，则仅由于速度垂直于磁场的分量而感应的电动势。

$$\mathrm{\mathit{e=B\:l\:v} \:sinθ\:\:\:\:\:\:...(4)}$$

数值例子

一根长度为 0.8 米的导体位于磁通密度为 2 $Wb/m^{2}$ 的均匀磁场中，并且与磁场成直角。导体以 30 m/s 的速度移动。计算导体中感应的电动势。如果导体与磁场成 45° 角移动，则感应的电动势是多少？

解答

• 情况 1 - 当导体垂直于磁场运动时。

• $$\mathrm{\mathit{e=B\:l\:v}=2\times(0.8)\times(30)=48V}$$

• 情况 2 - 当导体与磁场成 45° 角运动时。

• $$\mathrm{\mathit{e=B\:l\:v}\:sinθ=2\times(0.8)\times(30)\times sin45=33.95V}$$

Saini Manish Kumar

更新于：2021年7月23日

26K+ 浏览量

启动您的职业生涯

完成课程后获得认证

开始学习