数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究C++ 无向图中所有连通分量的最小元素之和
在这个问题中，我们得到一个包含 N 个数字的数组 arr，其中 arr[i] 代表第 (i+1) 个节点。此外，还有 M 对边，其中 u 和 v 代表由边连接的节点。我们的任务是创建一个程序来查找无向图中所有连通分量的最小元素之和。如果一个节点与任何其他节点都没有连接，则将其计为只有一个节点的连通分量。
让我们来看一个例子来理解这个问题：
输入
arr[] = {2, 7, 5, 1, 2} m = 2
1 2
4 5输出
8
解释
以下是上面描述的图：
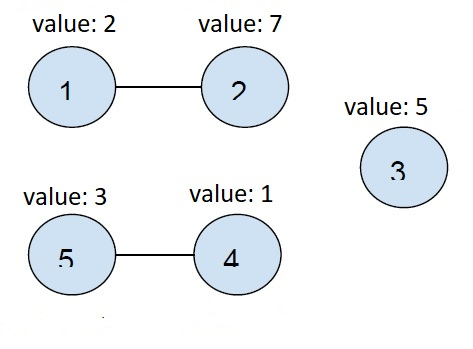
我们有两个连接的节点和一个单个节点。
因此，让我们取所有连通分量的最小值。
Min (节点1 和 节点2) = min (2, 7) = 2
Min (节点4 和 节点5) = min (1, 3) = 1
Min (节点3) = min (5) = 5
总和 = 1 + 2 + 5 = 8
为了解决这个问题，我们将使用任何遍历技术（BFS 或 DFS）查找无向图的所有连通节点，然后为所有已访问的节点创建一个已访问数组，以避免重复访问。在访问直接或间接连接的连通节点时，我们将找到所有连接的最小值。并将此最小值添加到 sum 变量中。访问所有节点后，我们将打印 sum。
示例
程序演示了我们解决方案的工作原理：
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
vector<int> graph[N];
bool visited[N];
void dfs(int node, int arr[], int minimum){
minimum = min(minimum, arr[node]);
visited[node] = true;
for (int i : graph[node]) {
if (!visited[i])
dfs(i, arr, minimum);
}
}
void createEdge(int u, int v){
graph[u - 1].push_back(v - 1);
graph[v - 1].push_back(u - 1);
}
int minSum(int arr[], int n){
int sum = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
int minimum = arr[i];
dfs(i, arr, minimum);
sum += minimum;
}
}
return sum;
}
int main(){
int arr[] = {2, 7, 5, 1, 3};
createEdge(1, 2);
createEdge(4, 5);
int n = sizeof(arr) / sizeof(arr[0]);
cout<<"The sum of minimum elements in all connected components of an undirected graph is ";
cout<<minSum(arr, n);
return 0;
}输出
The sum of minimum elements in all connected components of an undirected graph is 8
更新于：2020年8月6日
361 次查看
广告