数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 迷宫 II
假设在一个迷宫中有一个球，迷宫中有空的空间和墙壁。现在球可以通过滚动任何方向（例如上、下、左或右）穿过空路径，但它不会停止滚动，直到撞到墙壁。当球停止时，它可以选择下一个方向。
我们必须给出球的起始位置、目的地和迷宫，我们必须找到球到达目的地的最短距离。这里的距离实际上是由球覆盖的空单元格的数量定义的（不包括起始位置，包括起始位置）。如果无法让球停在目的地，则返回 -1。
迷宫由一个二维数组表示。这里 1 表示墙壁，0 表示空空间。迷宫的边界都是墙壁。起始和目标坐标由行和列索引表示。
因此，如果输入类似于由二维数组表示的迷宫
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 |
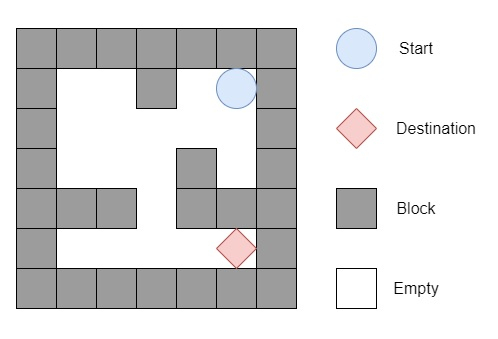
起始位置为 (0, 4) 目标位置为 (4, 4)，则输出将为 12，一种可能的方式是：左到下到左到下到右到下到右。(1+1+3+1+2+2+2) = 12
为了解决这个问题，我们将遵循以下步骤：
n := 行数，m := 列数
ret := 无穷大
定义一个 n x m 阶的二维数组 dist
定义一个队列 q
将起点插入 q
dist[start[0], start[1]] := 0
当 (q 不为空) 时，执行：
curr := q 的第一个元素
从 q 中删除元素
x := curr[0], y := curr[1]
如果 x 等于 destination[0] 且 y 等于 destination[1]，则：
ret := ret 和 dist[x, y] 的最小值
currDist := dist[x, y]
tempDist := 0
i := x
当 (i + 1 < n 且 grid[i + 1, y] 为零) 时，执行：
(i 加 1)
(tempDist 加 1)
如果 currDist + tempDist < dist[i, y]，则：
dist[i, y] := currDist + tempDist
将 { i, y } 插入 q
i := x
tempDist := 0
当 (i - 1 >= 0 且 grid[i - 1, y] 为零) 时，执行：
(tempDist 加 1)
(i 减 1)
如果 currDist + tempDist *lt; dist[i, y]，则：
dist[i, y] := currDist + tempDist
将 { i, y } 插入 q
i := y
tempDist := 0
当 (i - 1 >= 0 且 grid[x, i - 1] 为零) 时，执行：
(i 减 1)
(tempDist 加 1)
如果 currDist + tempDist < dist[x, i]，则：
dist[x, i] := currDist + tempDist
将 { x, i } 插入 q
i := y
tempDist := 0
当 (i + 1 < m 且 grid[x, i + 1] 为零) 时，执行：
(i 加 1)
(tempDist 加 1)
如果 currDist + tempDist < dist[x, i]，则：
dist[x, i] := currDist + tempDist
将 { x, i } 插入 q
返回 (如果 ret 等于 inf，则返回 -1，否则返回 ret)
示例
让我们看看以下实现以获得更好的理解：
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int shortestDistance(vector<vector<int<>& grid, vector<int<& start, vector<int<& destination) {
int n = grid.size();
int m = n? grid[0].size() : 0;
int ret = INT_MAX;
vector < vector <int< > dist(n, vector <int<(m, INT_MAX));
queue < vector <int< > q;
q.push(start);
dist[start[0]][start[1]] = 0;
while(!q.empty()){
vector <int< curr = q.front();
q.pop();
int x = curr[0];
int y = curr[1];
if(x == destination[0] && y == destination[1]){
ret = min(ret, dist[x][y]);
}
int currDist = dist[x][y];
int tempDist = 0;
int i = x;
while(i + 1 < n && !grid[i + 1][y]){
i++;
tempDist++;
}
if(currDist + tempDist < dist[i][y]){
dist[i][y] = currDist + tempDist;
q.push({i, y});
}
i = x;
tempDist = 0;
while(i - 1 >= 0 && !grid[i - 1][y]){
tempDist++;
i--;
}
if(currDist + tempDist < dist[i][y]){
dist[i][y] = currDist + tempDist;
q.push({i, y});
}
i = y;
tempDist = 0;
while(i - 1 >= 0 && !grid[x][i - 1]){
i--;
tempDist++;
}
if(currDist + tempDist < dist[x][i]){
dist[x][i] = currDist + tempDist;
q.push({x, i});
}
i = y;
tempDist = 0;
while(i + 1 < m && !grid[x][i + 1]){
i++;
tempDist++;
}
if(currDist + tempDist < dist[x][i]){
dist[x][i] = currDist + tempDist;
q.push({x, i});
}
}
return ret == INT_MAX ? - 1 : ret;
};
main(){
Solution ob;
vector<vector<int<> v = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,1,0},{1,1,0,1,1},{0,0,0,0,0}};
vector<int< v1 = {0,4}, v2 = {4,4};
cout << (ob.shortestDistance(v, v1, v2));
}输入
{{0,0,1,0,0},{0,0,0,0,0},{0,0,0,1,0},{1,1,0,1,1},{0,0,0,0,0}}, {0,4},{4,4}输出
12
455 次浏览
