数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究C++ 迷宫 III
假设有一个迷宫，其中包含空的空间和墙壁，迷宫中还有一个球。球可以通过向上 (u)、向下 (d)、向左 (l) 或向右 (r) 滚动穿过空的空间，但它会一直滚动直到碰到墙壁。当球停止时，它可以选择下一个方向。迷宫中还有一个洞。如果球滚到洞上，它就会掉进洞里。
因此，如果我们有球的位置、洞的位置和迷宫，我们必须找出球如何通过移动最短距离掉入洞中。这里的距离由球从起点（不包括）到洞（包括）经过的空空间的数量定义。
使用 'u'、'd'、'l' 和 'r' 返回移动方向。由于可能存在几种不同的最短路径，输出应为字典序最小的路径。如果球无法到达洞，则显示“impossible”。
这里迷宫由一个二进制矩阵表示。1 表示墙壁，0 表示空空间。球和洞的坐标由行和列索引表示。
所以，如果输入像这样
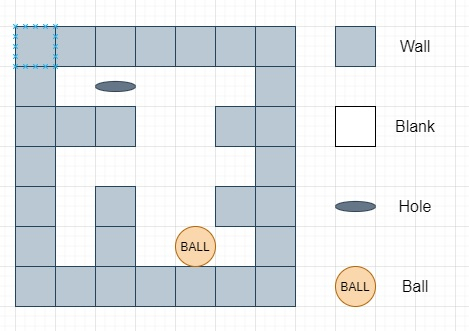
则输出将为 'lul'，表示先向左移动，然后向上，再向左，另一个结果可能是 'ul'，先向上再向左，两者长度均为 6，但它在字典序上不小于 'lul'
为了解决这个问题，我们将遵循以下步骤：
定义一个名为 Data 的数据类型，它将包含距离、字符串 d 和坐标 x、y。
定义一个大小为 4 x 2 的数组 dir：={{1, 0}, {0, - 1}, {0, 1}, { - 1, 0}}
定义一个大小为 4 的数组 dirst：={'d', 'l', 'r', 'u'}
定义一个函数 ok()，它将接收 x1、y1、x2、y2，
如果 x1 等于 x2 且 y1 等于 y2，则返回 true
从主方法执行以下操作：
n := 迷宫的行大小
m := （如果 n 不为零，则为迷宫的列大小，否则为 0）
定义一个优先级队列 pq
将新的数据 (0, ball[0], ball[1], "") 插入 pq
定义一个大小为 n x m 的二维数组 visited
当 (pq 不为空) 时，执行以下操作：
curr := pq 的顶部元素
x := curr.x
y := curr.y
dist := curr.dist
d := curr.d
如果 ok(x, y, hole[0], hole[1])，则：
返回 d
visited[x, y] := true
从 pq 中删除元素
从 k 初始化为 0，当 k - 4 时，更新（k 增加 1），执行以下操作：
nx := x，ny := y
tempDist := 0
当 nx + dir[k, 0] < n 且 nx + dir[k, 0] >= 0 且 ny + dir[k, 1] < m 且 ny + dir[k, 1] >= 0 且 maze[nx + dir[k, 0], ny + dir[k, 1]] 为 0 时，执行以下操作：
nx := nx + dir[k, 0]
ny := ny + dir[k, 1]
（tempDist 增加 1）
如果 ok(nx, ny, hole[0], hole[1])，则：
退出循环
如果 visited[nx, ny] 为零，则：
将新的 Data(dist + tempDist, nx, ny, d + dirst[k]) 插入 pq
返回“impossible”
示例
让我们看看下面的实现，以便更好地理解：
#include <bits/stdc++.h>
using namespace std;
int dir[4][2] = {{1, 0}, {0, -1}, {0, 1}, {-1, 0}};
char dirst[4] = {'d', 'l', 'r', 'u'};
class Solution {
public:
struct Data {
int dist;
string d;
int x, y;
Data(int a, int b, int c, string s) {
d = s;
dist = a;
x = b;
y = c;
}
};
struct Comparator {
bool operator()(Data a, Data b) {
return a.dist != b.dist ? !(a.dist < b.dist) : !(a.d < b.d);
}
};
bool ok(int x1, int y1, int x2, int y2) { return x1 == x2 && y1 == y2; }
string findShortestWay(vector<vector<int>> &maze, vector<int>&ball,
vector<int> &hole) {
int n = maze.size();
int m = n ? maze[0].size() : 0;
priority_queue<vector<Data>, vector<Data>, Comparator> pq;
pq.push(Data(0, ball[0], ball[1], ""));
vector<vector<bool>> visited(n, vector<bool>(m));
while (!pq.empty()) {
Data curr = pq.top();
int x = curr.x;
int y = curr.y;
int dist = curr.dist;
string d = curr.d;
if (ok(x, y, hole[0], hole[1])) {
return d;
}
visited[x][y] = true;
pq.pop();
for (int k = 0; k < 4; k++) {
int nx = x;
int ny = y;
int tempDist = 0;
while (nx + dir[k][0] < n && nx + dir[k][0] >= 0 && ny + dir[k][1] < m && ny + dir[k][1] >= 0 && !maze[nx + dir[k][0]][ny + dir[k][1]]) {
nx += dir[k][0];
ny += dir[k][1];
tempDist++;
if (ok(nx, ny, hole[0], hole[1]))
break;
}
if (!visited[nx][ny]) {
pq.push(Data(dist + tempDist, nx, ny, d + dirst[k]));
}
}
}
return "impossible";
}
};
main() {
Solution ob;
vector<vector<int>> v = {
{0, 0, 0, 0, 0},
{1, 1, 0, 0, 1},
{0, 0, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 1, 0, 0, 0}};
vector<int> v1 = {4, 3}, v2 = {0, 1};
cout << (ob.findShortestWay(v, v1, v2));
}输入
vector<vector<int>> v = {{0, 0, 0, 0, 0},
{1, 1, 0, 0, 1},
{0, 0, 0, 0, 0},
{0, 1, 0, 0, 1},
{0, 1, 0, 0, 0}};
vector<int> v1 = {4, 3}, v2 = {0, 1};输出
lul
407 次浏览
