数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究图的类型
根据顶点数、边数、互连性和整体结构，图有多种类型。本章将仅讨论其中几种重要的图类型。
空图
**没有边的图**称为空图。
示例
在上图中，有三个顶点，分别命名为“a”、“b”和“c”，但它们之间没有边。因此，它是一个空图。
平凡图
**只有一个顶点的图**称为平凡图。
示例
在上图中，只有一个顶点“a”，没有其他边。因此，它是一个平凡图。
无向图
无向图包含边，但这些边不是有向边。
示例
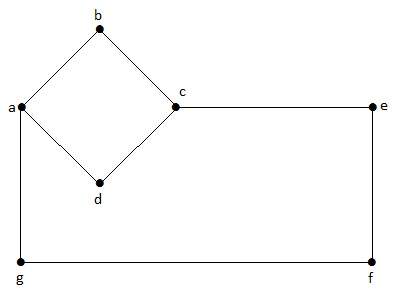
在此图中，“a”、“b”、“c”、“d”、“e”、“f”、“g”是顶点，“ab”、“bc”、“cd”、“da”、“ag”、“gf”、“ef”是图的边。由于它是一个无向图，“ab”和“ba”是相同的。其他边也以相同的方式考虑。
有向图
在有向图中，每条边都有一个方向。
示例
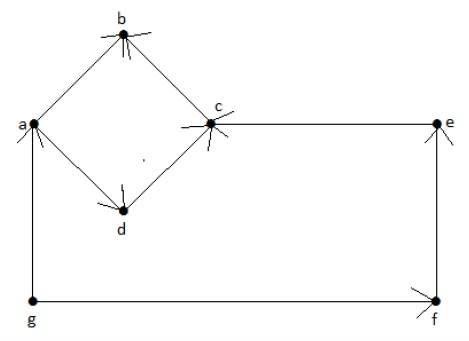
在上图中，我们有七个顶点“a”、“b”、“c”、“d”、“e”、“f”和“g”，以及八条边“ab”、“cb”、“dc”、“ad”、“ec”、“fe”、“gf”和“ga”。由于它是一个有向图，每条边都带有箭头标记，表示其方向。请注意，在有向图中，“ab”与“ba”不同。
简单图
**没有环**且**没有平行边**的图称为简单图。
具有“n”个顶点的单个图中可能存在的最大边数为nC2，其中nC2 = n(n – 1)/2。
具有“n”个顶点的简单图的个数为2nc2 = 2n(n-1)/2。
示例
在下图中，有 3 个顶点和 3 条边，这是排除平行边和环的最大值。这可以通过使用上述公式来证明。
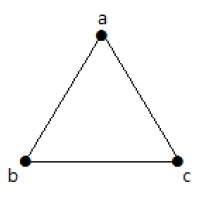
具有 n=3 个顶点的最大边数 -
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
具有 n = 3 个顶点的简单图的最大数量 -
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
这 8 个图如下所示 -
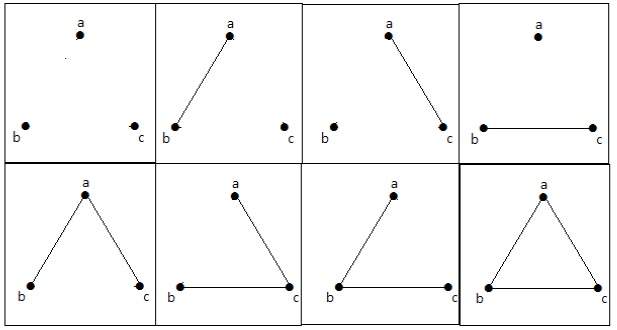
连通图
如果**每对顶点之间都存在一条路径**，则称图 G 为连通图。图中每个顶点至少应有一条边。这样我们就可以说它连接到边另一侧的某个其他顶点。
示例
在下图中，每个顶点都有自己的边连接到其他边。因此，它是一个连通图。
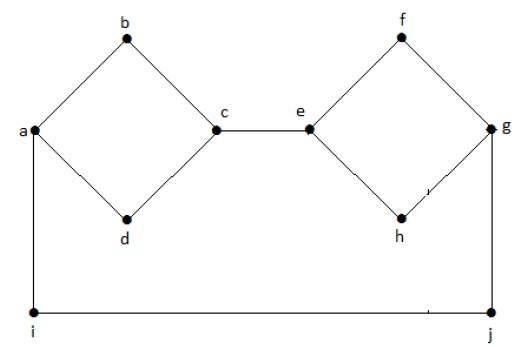
非连通图
如果图 G 不包含至少两个连通顶点，则称其为非连通图。
示例 1
下图是非连通图的一个示例，其中有两个连通分量，一个包含“a”、“b”、“c”、“d”顶点，另一个包含“e”、“f”、“g”、“h”顶点。
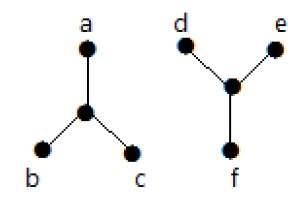
这两个连通分量是独立的，并且彼此不连接。因此，它被称为非连通图。
示例 2
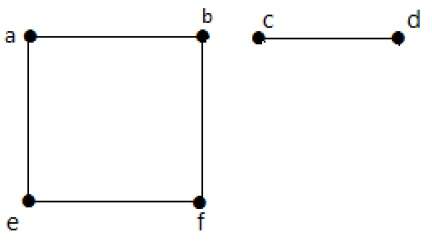
在此示例中，有两个独立的连通分量，a-b-f-e 和 c-d，它们彼此不连接。因此，这是一个非连通图。
正则图
如果**所有顶点的度数都相同**，则称图 G 为正则图。如果图中每个顶点的度数为“k”，则该图称为“k-正则图”。
示例
在下图中，所有顶点都具有相同的度数。因此，这些图称为正则图。
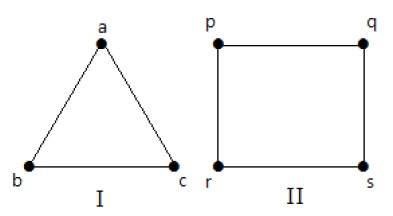
在这两个图中，所有顶点的度数均为 2。它们称为 2-正则图。
完全图
具有“n”个互连顶点的简单图称为完全图，并用“Kn”表示。在图中，**一个顶点应与所有其他顶点都有边相连**，然后它被称为完全图。
换句话说，如果一个顶点连接到图中的所有其他顶点，则它被称为完全图。
示例
在下图中，图中的每个顶点都与图中除自身以外的所有其他顶点相连。
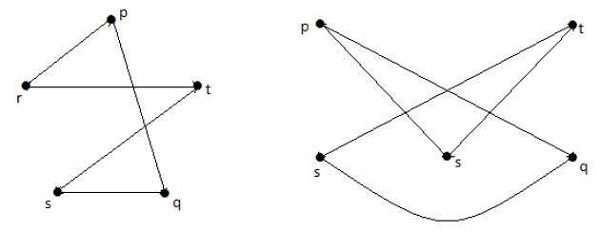
在图 I 中，
| a | b | c | |
|---|---|---|---|
| a | 未连接 | 已连接 | 已连接 |
| b | 已连接 | 未连接 | 已连接 |
| c | 已连接 | 已连接 | 未连接 |
在图 II 中，
| p | q | r | s | |
|---|---|---|---|---|
| p | 未连接 | 已连接 | 已连接 | 已连接 |
| q | 已连接 | 未连接 | 已连接 | 已连接 |
| r | 已连接 | 已连接 | 未连接 | 已连接 |
| s | 已连接 | 已连接 | 已连接 | 未连接 |
环图
如果一个简单图具有“n”个顶点（n >= 3）和“n”条边，并且所有边都形成长度为“n”的环，则该图称为环图。
如果**图中每个顶点的度数为二**，则称为环图。
**符号** - Cn
示例
请查看以下图表 -
图 I 有 3 个顶点和 3 条边，形成一个环“ab-bc-ca”。
图 II 有 4 个顶点和 4 条边，形成一个环“pq-qs-sr-rp”。
图 III 有 5 个顶点和 5 条边，形成一个环“ik-km-ml-lj-ji”。
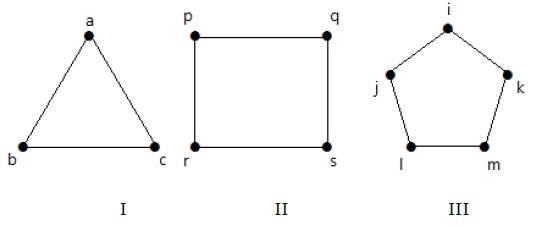
因此，所有给定的图都是环图。
轮图
轮图是从环图 Cn-1 通过添加一个新顶点获得的。该新顶点称为**中心**，它连接到 Cn 的所有顶点。
**符号** - Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
示例
请查看以下图表。它们都是轮图。
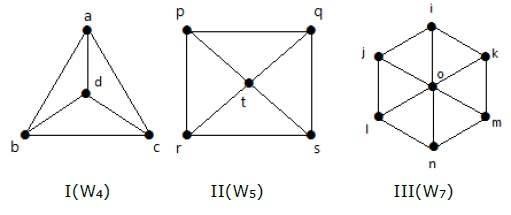
在图 I 中，它是从 C3 通过在中间添加一个名为“d”的顶点获得的。它表示为 W4。
Number of edges in W4 = 2(n-1) = 2(3) = 6
在图 II 中，它是从 C4 通过在中间添加一个名为“t”的顶点获得的。它表示为 W5。
Number of edges in W5 = 2(n-1) = 2(4) = 8
在图 III 中，它是从 C6 通过在中间添加一个名为“o”的顶点获得的。它表示为 W7。
Number of edges in W4 = 2(n-1) = 2(6) = 12
有环图
**至少有一个**环的图称为有环图。
示例
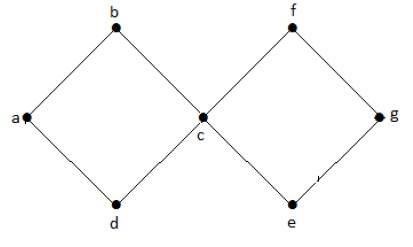
在上图示例中，我们有两个环 a-b-c-d-a 和 c-f-g-e-c。因此，它被称为有环图。
无环图
**没有环**的图称为无环图。
示例
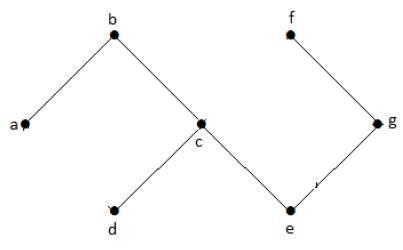
在上图示例中，我们没有任何环。因此，它是一个无环图。
二分图
顶点划分 V = {V1, V2} 的简单图 G = (V, E) 称为二分图，**如果 E 的每条边都连接 V1 中的一个顶点到 V2 中的一个顶点**。
通常，二分图有两组顶点，假设为 V1 和 V2，如果画一条边，它应该连接集合 V1 中的任何顶点到集合 V2 中的任何顶点。
示例
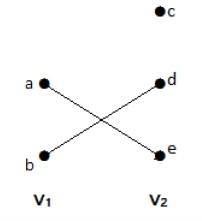
在此图中，您可以观察到两组顶点 - V1 和 V2。这里，名为“ae”和“bd”的两条边连接了两组顶点 V1 和 V2。
完全二分图
如果划分 V = {V1, V2} 的二分图“G”，G = (V, E) 使得 V1 中的每个顶点都连接到 V2 的每个顶点，则称其为完全二分图。
通常，完全二分图将集合 V1 中的每个顶点连接到集合 V2 中的每个顶点。
示例
下图是一个完全二分图，因为它具有连接集合 V1 中的每个顶点到集合 V2 中的每个顶点的边。
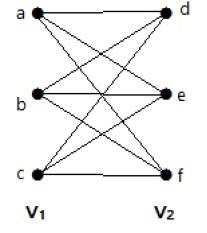
如果 |V1| = m 且 |V2| = n，则完全二分图表示为 Km, n。
Km,n 有 (m+n) 个顶点和 (mn) 条边。
如果 m=n，则 Km,n 是一个正则图。
通常，**完全二分图不是完全图**。
如果 m = n = 1，则 Km,n 是一个完全图。
具有**n**个顶点的二分图中的最大边数为
如果 n = 10，k5, 5 = ⌊ n2 4 ⌋ = ⌊ 102 4 ⌋ = 25
类似地，K6，4=24
K7，3=21
K8，2=16
K9，1=9
如果n=9，k5，4 = ⌊ n2 4 ⌋ = ⌊ 92 4 ⌋ = 20
类似地，K6，3=18
K7，2=14
K8，1=8
如果图'G'没有奇数长度的环路，则'G'是二分图。二分图的一种特殊情况是**星形图**。
星形图
形式为K1, n-1的完全二分图是具有n个顶点的星形图。如果一个顶点属于一个集合，而所有其余顶点属于另一个集合，则星形图是完全二分图。
示例
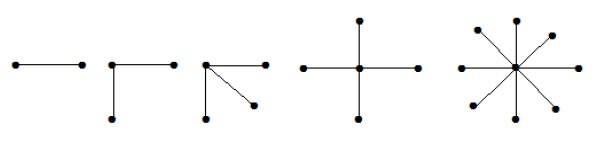
在上图中，在'n'个顶点中，所有'n-1'个顶点都连接到一个顶点。因此，它采用K1, n-1的形式，这些都是星形图。
896次浏览
