数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究什么是功率谱密度？
功率谱密度
信号 $x\mathrm{\left(\mathit{t}\right)}$ 在频域中的平均功率分布称为功率谱密度 (PSD) 或功率密度 (PD) 或功率密度谱。PSD 函数用 $\mathit{S\mathrm{\left({\mathit{\omega }}\right)}}$ 表示，由下式给出：
$$\mathrm{\mathit{S}\mathrm{\left(\mathit{\omega}\right)}\mathrm{=}\displaystyle\lim_{\tau \to \infty }\frac{\left| \mathit{X\mathrm{\left ( \mathit{\omega}\right)}}\right|^{2}}{\tau}\:\:\:\:\:\:...(1)}$$
解释
为了推导出功率谱密度 (PSD) 函数，将功率信号视为能量信号的极限情况，即信号 $\mathit{Z\mathrm{\left({\mathit{t }}\right)}}$ 在区间 $\left|\tau /2 \right|$ 外为零，如图所示。
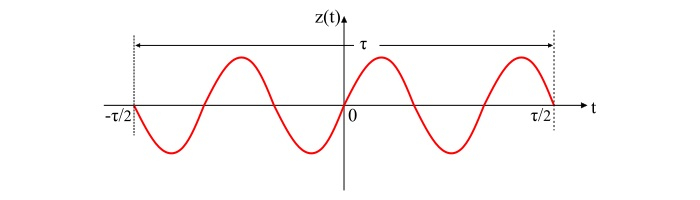
信号 $\mathit{Z\mathrm{\left({\mathit{t }}\right)}}$ 由下式给出：
$$\mathrm{\mathit{Z\mathrm{\left({\mathit{t }}\right)}}\mathrm{=}\begin{cases} x\mathrm{\left(\mathit{t}\right)}\:\left|t \right|<\left ( \frac{\tau }{2} \right )\ 0 \:\:\: {\mathrm{otherwise} } \end{cases}}$$
其中，$x\mathrm{\left(\mathit{t}\right)}$ 是相同幅度的功率信号，延伸到无穷大。
由于信号 $\mathit{Z\mathrm{\left({\mathit{t }}\right)}}$ 是持续时间为 $\tau$ 的有限持续时间信号，因此它是一个具有能量 E 的能量信号，由下式给出：
$$\mathrm{\mathit{E}\:\mathrm{=}\:\int_{-\infty}^{\infty}\left|\mathit{Z\mathrm{\left ( \mathit{t} \right )}}\right|^{2}\:\mathit{dt}\:\mathrm{=}\:\frac{1}{2\pi}\int_{-\infty }^{\infty}\left| \mathit{Z}\mathrm{\left ( \mathit{\omega } \right )}\right|^{2}\:\mathit{d\omega }}$$
其中，
$$\mathrm{\mathit{Z\mathrm{\left({\mathit{t }}\right)}}\overset{\mathit{FT}}{\leftrightarrow}\mathit{Z\mathrm{\left({\mathit{\omega}}\right)}}}$$
另外，
$$\mathrm{\int_{-\infty}^{\infty}\left|\mathit{Z\mathrm{\left ( \mathit{t} \right )}}\right|^{2}\:\mathit{dt}\:\mathrm{=}\:\int_{-\mathrm{\left(\tau/2\right)}}^{\mathrm{\left(\tau /2 \right)}}\left| \mathit{x}\mathrm{\left ( \mathit{t} \right)}\right|^{2}\:\mathit{dt}}$$
因此，我们有：
$$\mathrm{\frac{1}{\mathit{\tau}}\int_{-\mathrm{\left(\tau/2\right)}}^{\mathrm{\left(\tau /2 \right )}}\left| \mathit{x}\mathrm{\left ( \mathit{t} \right )}\right|^{2}\:\mathit{dt}\:\mathrm{=}\:\frac{1}{2\pi}\mathrm{\left(\frac{1}{\tau}\right)}\int_{-\infty }^{\infty}\left| \mathit{Z}\mathrm{\left ( \mathit{\omega } \right )}\right|^{2}\:\mathit{d\omega}}$$
因此，当 $\tau\to \infty $ 时，上述等式的左侧给出信号 $x\mathrm{\left(\mathit{t}\right)}$ 的平均功率 (P)，即：
$$\mathrm{\mathit{P}\:\mathrm{=}\:\frac{1}{2\pi}\int_{-\infty}^{\infty}\displaystyle \lim_{\tau \to\infty}\left(\frac{\left| \mathit{Z}\mathrm{\left ( \mathit{\omega } \right )}\right|^{2}}{\tau}\right)\:\mathit{d\omega}\:\:\:\:\:\:...(2)}$$
如果 $\tau\to \infty $，则等式 (2) 中的 $\left(\frac{\left| Z\mathrm{\left ( \mathit{\omega } \right )}\right|^{2}}{\tau}\right)$ 接近一个有限值。假设此有限值由 $\mathrm{\mathit{S}\mathrm{\left(\mathit{\omega}\right)}}$ 表示，即：
$$\mathrm{\mathit{S}\mathrm{\left(\mathit{\omega}\right)}\:\mathrm{=}\:\displaystyle \lim_{\tau \to\infty}\left(\frac{\left| \mathit{Z}\mathrm{\left ( \mathit{\omega } \right )}\right|^{2}}{\tau}\right) \:\:\:\:\:\:...(3)}$$
等式 (3) 中的表达式称为信号 $z\mathrm{\left(\mathit{t}\right)}$ 的功率谱密度 (PSD)。因此，对于函数 $x\mathrm{\left(\mathit{t}\right)}$，PSD 函数由下式给出：
$$\mathrm{\mathit{S}\mathrm{\left(\mathit{\omega}\right)}\:\mathrm{=}\:\displaystyle \lim_{\tau \to\infty}\left(\frac{\left| \mathit{X}\mathrm{\left ( \mathit{\omega } \right )}\right|^{2}}{\tau}\right)\:\:\:\:\:\:...(4)}$$
因此，信号 $x\mathrm{\left(\mathit{t}\right)}$ 的平均功率 (P) 由下式给出：
$$\mathrm{\mathit{P}\mathrm{=}\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathit{S}\mathrm{\left(\mathit{\omega}\right)}\:\mathit{d\omega }\:\mathrm{=}\:\int_{-\infty}^{\infty}\mathit{S}\mathrm{\left(\mathit{f}\right)}\:\mathit{df}\:\:\:\:\:\:...(5)}$$
此外，周期函数的功率谱密度 (PSD) 由下式给出：
$$\mathrm{\mathit{S}\mathrm{\left(\mathit{\omega}\right)}\:\mathrm{=}\:2\pi\:\sum_{\mathit{n}=-\infty }^{\infty}\left|\mathit{c_{n}}\right|^{2}\delta \mathrm{\left(\mathit{\omega -n\omega _{\mathrm{0}}} \right )}}\:\:\:\:\:\:...(6)$$
功率谱密度 (PSD) 的特性
特性 1 - 对于功率信号，功率谱密度曲线下的面积等于该信号的平均功率，即：
$$\mathrm{\mathit{P}\:\mathrm{=}\:\frac{1}{2\pi}\int_{-\infty}^{\infty}\mathit{S}\mathrm{\left(\mathit{\omega}\right)}\:\mathit{d\omega }}$$
特性 2 - 如果信号 $x\mathrm{\left(\mathit{t}\right)}$ 是输入到具有脉冲响应 $h\mathrm{\left(\mathit{t}\right)}$ 的 LTI 系统，则系统的输入和输出 PSD 函数的关系为：
$$\mathrm{\mathit{S}_{y}\mathrm{\left(\mathit{\omega}\right)}\:\mathrm{=}\:\left|\mathit{H}\left(\mathit{\omega}\right)\right|^{2}\:\mathit{S}_{\mathit{x}}\mathrm{\left(\mathit{\omega}\right)}}$$
其中，$\left|\mathit{H}\left(\mathit{\omega}\right)\right|$ 是系统传递函数的幅度。
特性 3 - 自相关函数 $R\mathrm{\left(\mathrm{\tau}\right)}$ 和功率信号的功率谱密度函数 $\mathit{S}\mathrm{\left(\mathit{\omega}\right)}$ 构成傅里叶变换对，即：
$$\mathrm{\mathit{R\mathrm{\left({\mathit{\tau }}\right)}}\overset{\mathit{FT}}{\leftrightarrow}\mathit{S\mathrm{\left({\mathit{\omega}}\right)}}}$$
24K+ 浏览量
