数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学使用 Matplotlib 在 Python 中绘制交叉谱密度
使用 Python 进行交叉谱密度分析提供了一种有效的方法来理解信号的频率特性和相互关系。在本文中，我们将深入探讨使用 Python 和 Matplotlib 绘制交叉谱密度的方法。通过利用这些库的功能，我们可以直观地表示频谱并揭示信号之间的关系。
通过系统的方法，我们将说明如何生成随机信号、计算它们的交叉谱密度以及创建有见地的可视化效果。
什么是交叉谱密度？
交叉谱密度是一种数学度量，用于检查两个信号的频率特性和相互关系。它提供了关于一个信号在不同频率下的功率与另一个信号在相同频率下的功率之间对应关系的见解。
通过计算交叉谱密度，可以检测信号之间是否存在共享的或相关的频率成分，从而可以评估它们的相互影响或依赖性。这种分析技术在信号处理、通信系统和振动分析等不同领域具有重要意义。
如何在 Python 中绘制交叉谱密度？
以下是我们将遵循的步骤，以便在 Python 中绘制交叉谱密度：
我们导入必要的库：numpy 用于数值计算，matplotlib.pyplot 用于绘图。
我们设置随机数生成器的种子以确保可重复性。
我们为信号定义样本数 (N) 和时间步长 (dt)。我们还使用 numpy 的 arange 函数创建一个时间向量 t。
我们生成两个信号：
信号 1 (x1) 是频率为 5 Hz、幅度为 1 的正弦波。
信号 2 (x2) 使用 numpy.random.normal 函数生成，该函数生成具有指定均值和标准差的正态（高斯）分布的随机样本。在本例中，我们使用均值为 0、标准差为 1 来生成白噪声。
我们使用 matplotlib.pyplot 中的 plt.csd 函数计算交叉谱密度。此函数将两个信号 (x1 和 x2) 作为输入，以及用于快速傅里叶变换 (FFT) 计算的点数 (NFFT) 和采样频率 (Fs)。
我们使用 plt.semilogy 绘制交叉谱密度，它以对数刻度绘制 y 轴，以便更好地可视化。频率值 (frequencies) 和交叉谱密度的绝对值 (np.abs(Cxy)) 作为参数传递给绘图函数。
我们使用 plt.xlabel 和 plt.ylabel 为 x 轴和 y 轴添加标签，并使用 plt.title 设置绘图的标题。
我们使用 plt.grid(True) 在绘图上启用网格线。
最后，我们使用 plt.show() 显示绘图。
通过修改 x1 和 x2 信号的生成方式，您可以分析不同类型信号或现实世界数据之间的交叉谱密度。
以下是使用上述步骤的程序示例。在这个示例中，我们生成了两个信号：一个正弦波 (x1) 和一个白噪声 (x2)。然后，我们使用 Matplotlib 的 plt.csd 函数计算交叉谱密度。NFFT 参数指定 FFT 计算中每个块中使用的点数，Fs 表示采样频率。
示例
import numpy as np
import matplotlib.pyplot as plt
# Generate two random signals
np.random.seed(0)
N = 1000 # Number of samples
dt = 0.01 # Time step
t = np.arange(0, N*dt, dt) # Time vector
# Signal 1: Sine wave
f1 = 5 # Frequency of the sine wave
A1 = 1 # Amplitude of the sine wave
x1 = A1 * np.sin(2*np.pi*f1*t)
# Signal 2: White noise
mean = 0
std_dev = 1
x2 = np.random.normal(mean, std_dev, N)
# Compute the cross-spectral density
frequencies, Cxy = plt.csd(x1, x2, NFFT=1024, Fs=1/dt)
# Plot the cross-spectral density
plt.figure()
plt.semilogy(frequencies, np.abs(Cxy), 'r')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Cross-Spectral Density')
plt.title('Cross-Spectral Density')
plt.grid(True)
plt.show()
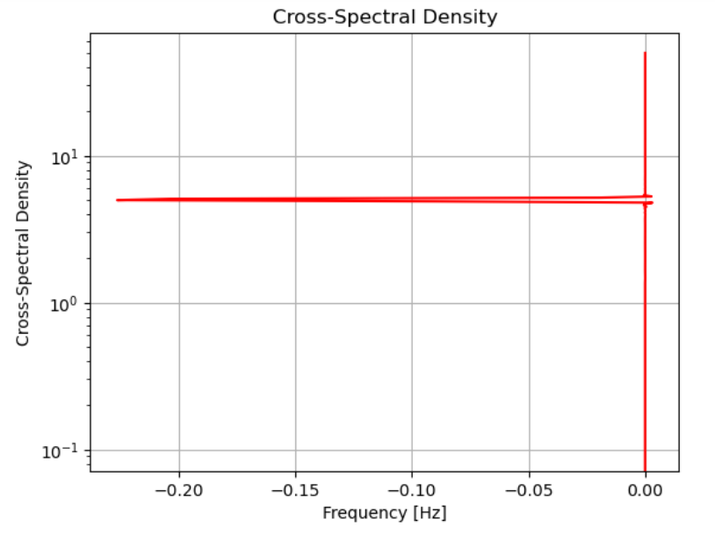
输出
结论
总而言之，Python 和 Matplotlib 提供了一套宝贵的工具来绘制交叉谱密度，方便分析和可视化信号的频率特性和相互关系。通过遵循本文中提供的分步指南，专业人士和研究人员可以轻松地生成随机信号、计算它们的交叉谱密度并生成有意义的可视化表示。
这种能力使人们能够深刻理解信号之间的关系，使其成为信号处理、实验数据分析和科学研究等不同领域的重要资产。
浏览量：399
