积分的应用

---

简介

积分的应用广泛应用于数学、科学、工程等各个领域。积分的应用在数学和物理学中被广泛用于各种目的。

• 如果积分应用于曲线下的面积或两条曲线之间的面积，则称为**积分的几何应用**，其中还包括求旋转体的体积、曲线的长度等。

• 如果积分应用于求物体的重心、质量、动量、位移、速度等，则称为**积分的物理应用**。

在本教程中，我们将学习积分及其在曲线下面积和两条曲线之间面积中的应用，并附带一些已解决的示例。

积分

等于曲线或函数下方的面积的数值可以称为**积分**。据说它们为解释面积、体积等的函数分配值，因为它们测量给定区间内的整个空间。

面积 A 由下式给出：

$$\mathrm{A = \int_{x=a}^{x=b}f(x) dx}$$

积分被称为找到这些积分的过程。积分有两种类型，即定积分和不定积分。带有极限的积分函数称为定积分。

定积分定义为：

$$\mathrm{I=\int_{x=a}^{x=b}f(x) dx}$$

没有极限的积分函数称为不定积分。

不定积分定义为：

$$\mathrm{\int_{x=a}^{x=b}f(x) dx=F(x)+C\: where\: C\: is\: a\: constant.}$$

积分的应用：曲线下面积

曲线 f(x) 下方的面积 A 在区间 [a, b] 内。我们需要在 a 和 b 的限制范围内对 f(x) 进行积分以找到 f(x) 下方的 A。由于积分函数具有限制 a 和 b，因此 f(x) 被称为定积分。

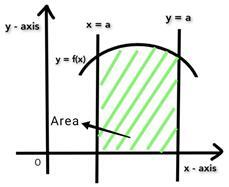
计算曲线下面积的公式由下式给出：

$$\mathrm{A = \int_{x=a}^{x=b}f(x) dx}$$

两条曲线之间的面积

两条曲线 f(x) 和 g(x) 在两点处相交。交点为 x= a 和 x=b，我们显然知道它们是 x 坐标。两条曲线在其之间包围了一个区域 A。

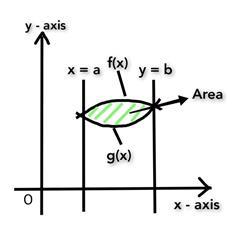
• 如果曲线 f(x) 高于 g(x)，使得对于 a≤ x ≤b，f(x) ≤g(x)，则

  求两条曲线之间面积的公式由下式给出：

  $$\mathrm{A = \int_{x=a}^{x=b}f(x) dx-\int_{x=a}^{x=b}g(x) dx}$$

• 如果曲线 g(x) 高于 f(x)，使得对于 a≤ x ≤b，g(x) ≤f(x)，则

  求两条曲线之间面积的公式由下式给出：

  $$\mathrm{A = \int_{x=a}^{x=b}g(x) dx-\int_{x=a}^{x=b}f(x) dx}$$

已解决的示例

1)求函数 f(x)=(x⁴+6) 曲线下的面积 A，给定限制为 2≤ x ≤3。

答案

计算曲线下面积的公式由下式给出：

曲线下的面积 = $\mathrm{\int_{x=a}^{x=b}f(x) dx}$

给定曲线下的面积 = $\mathrm{\int_2^3(x^4+6) dx}$

给定曲线下的面积 = $\mathrm{[\frac{x^5}{5}+6x]_{x=2}^{x=3}}$

给定曲线下的面积 = $\mathrm{[\frac{3^5}{5}-\frac{2^5}{5}] +[6(3)-6(2)]}$

给定曲线下的面积 = $\mathrm{[\frac{243-32}{5}] +[18-12]}$

给定曲线下的面积 =$\mathrm{\frac{211}{5}+6}$

给定曲线下的面积 = $\mathrm{\frac{211+30}{5}}$

给定曲线下的面积 = $\mathrm{\frac{241}{5}}$

给定曲线下的面积 = 48.1 平方单位。

因此，函数 (x⁴+6) 曲线下的面积为 48.1 平方单位。

2)求给定两条曲线 f(x)=3x 和 g(x)=2x 之间的面积 A，给定限制为 0≤ x ≤3。

答案

求两条曲线之间面积的公式由下式给出：

两条曲线之间的面积 $\mathrm{= \int_{x=a}^{x=b} f(x) dx-\int_{x=a}^{x=b}g(x) dx}$

给定曲线之间的面积 $\mathrm{= \int_0^3(3x-2x) dx}$

给定曲线之间的面积 = $\mathrm{\int_0^3x dx}$

给定曲线之间的面积 = $\mathrm{[\frac{x^2}{2}]_{x=0}^{x=3}}$

给定曲线之间的面积 = $\mathrm{\frac{(3)^2}{2}-0}$

给定曲线之间的面积 = $\mathrm{\frac{9}{2}}$

给定曲线之间的面积 = 4.5 平方单位。

因此，给定两条曲线 f(x)=3x 和 g(x)=2x 之间的面积 A 为 4.5 平方单位。

3)求函数 f(x)=(5x-x^2) 曲线下的面积 A，给定限制为 0≤ x ≤5。

答案

计算曲线下面积的公式由下式给出：

曲线下的面积 = $\mathrm{\int_{x=a}^{x=b}f(x) dx}$

给定曲线下的面积 = $\mathrm{\int_0^5(5x-x^2) dx}$

给定曲线下的面积 =$\mathrm{[\frac{5x^2}{2}+\frac{x^3}{3}]_{x=0}^{x=5}}$

给定曲线下的面积 = $\mathrm{[\frac{5(5)^2}{2}-\frac{5^3}{3}] -0}$

给定曲线下的面积 = $\mathrm{[\frac{125}{2}-\frac{125}{3}] -0}$

给定曲线下的面积 = $\mathrm{\frac{(3×125) - (2×125)}{6}}$

给定曲线下的面积 = $\mathrm{\frac{375 - 250}{6}}$

给定曲线下的面积 = $\mathrm{\frac{125}{6}}$

给定曲线下的面积 = 20.833 平方单位。

因此，函数 $\mathrm{\int_0^5(5x-x^2) dx}$ 曲线下的面积为 20.833 平方单位。

4)求给定两条曲线 f(x)=x⁴ 和 g(x)=x 之间的面积 A，给定限制为 2≤ x ≤3。

答案

求两条曲线之间面积的公式由下式给出：

$$\mathrm{A=\int_{x=a}^{x=b}f(x) dx-\int_{x=a}^{x=b}g(x) dx}$$

$$\mathrm{A=\int_2^3(x^4-x) dx}$$

$$\mathrm{A=[\frac{x^5}{5}-\frac{x^2}{2}]_{x=2}^{x=3}}$$

$$\mathrm{A=[\frac{3^5- 2^5}{5}]-[\frac{3^2-2^2}{2}]}$$

$$\mathrm{A=[\frac{243- 32}{5}]-[\frac{9-4}{2}]}$$

$$\mathrm{A=\frac{211}{5}-\frac{5}{2}}$$

$$\mathrm{A=\frac{422-25}{10}}$$

$$\mathrm{A=\frac{397}{10}}$$

$$\mathrm{A=39.7\: 平方单位.}$$

因此，给定两条曲线 f(x)=x⁴ 和 g(x)=x 之间的面积 A 为 39.7 平方单位。

结论

• 曲线下方的面积表示定义为积分。

• 定积分 I 由下式给出：

  $$\mathrm{I= \int_{x=a}^{x=b}f(x) dx}$$

• 没有极限的积分函数，例如 $\mathrm{\int_{x=a}^{x=b}f(x) dx=F(x)+C}$，称为不定积分。

• 计算曲线下面积的公式由下式给出：

  $$\mathrm{A =\int_{x=a}^{x=b}f(x) dx}$$

• 求两条曲线之间面积的公式由下式给出：

  $$\mathrm{面积=\int_{x=a}^{x=b}[f(x) -g(x)]dx}$$

常见问题解答

1. 哪些被认为是微积分的重要工具？

微积分的重要工具是积分、极限和导数。

它们的作用是描述函数的行为，然后对其进行分析。

历史上，在 17 世纪后期，著名的数学家艾萨克·牛顿爵士和戈特弗里德·莱布尼茨发现了微积分，因为他们为导数和微分的理论发展做出了贡献。

2. 谁引入了分部积分？

英国数学家布鲁克·泰勒以泰勒级数和定理而闻名，他是发现分部积分的人。由于这位伟大的数学家，我们有了一个新的分支，称为有限差分微积分。

3. 什么是曲面积分？

在弯曲的二维区域或平面上的积分称为曲面积分。

要定义函数 $\mathrm{\underline{F}}$ 的曲面积分，整个表面 S 被分成小的表面元素 ΔS。

$$\mathrm{\int F⋅ds=\lim_{n \rightarrow ∞} \sum_{i=1}^{n}\underline{F_i}\: \underline{ΔS_i} , \: ΔS→0}$$

4. 什么是线积分？

如果沿曲线计算积分的函数，则该积分称为线积分。

它也可以称为路径积分。

5. 重积分和曲面积分有什么区别？

在平坦的二维平面上的积分是重积分。而在弯曲的二维平面上的积分是曲面积分。