定积分的性质

---

引言

积分有两种方法：

• 确定积分和

• 不定积分。

定积分是在由边界指定的边界或区域上进行的。由于曲线是有限的，因此曲线下的面积也被认为是有限的，但不定积分用于没有上限或下限的函数，但由于函数本质上是无限的，因此上限和下限是不确定的。函数 + ∞ & -∞。

积分

• 在微积分中，我们关注的是寻找可微函数的导数（或微分）的方法。

• 我们能否解决逆问题？也就是说，如果函数具有给定的导数（或微分）？例如，函数 y=x⁶ 的导数是 $\mathrm{\frac{dy}{dx}=6x^5}$（或其微分是 $\mathrm{dy=6x^5 dx }$）。因此，很容易理解具有导数 $\mathrm{6x^5}$（或微分 $\mathrm{6x^5 dx}$）的函数是 x⁶ 。

• 在这种情况下，从导数 dy/dx=6x^5（或微分 dy=6x^5 dx）确定函数 y=x⁶ 的数学方法称为积分。

• 通过积分从函数的导数（或微分）获得的函数称为其积分。在上例中，$\mathrm{\frac{dy}{dx}=6x^5}$（或 $\mathrm{dy=6x^5 dx }$）的积分是 y=x⁶。显然，积分可以看作是反导数，即它是微分的逆过程。

定积分

如果在任何数学研究中的量都可以表示为一个级数的形式，通过根据某种规律或规则将其分成几个部分，使得级数的项数可以无限增加，并且级数的每一项都无限小，那么这样的级数的和的极限值称为定积分。

定积分作为和的极限

设 f(x) 是在有限区间 a≤x≤b 上定义的有界单值连续函数。现在，用点 a, a+h, a+2h,…., a+(n-1)h … a+nh 将区间 a≤x≤b 分成 n 个等长的子区间，每个子区间的长度为 h，其中 a+nh=b，或 nh=b-a。然后，极限（如果存在），

$$\mathrm{\displaystyle\lim \limits_{h\rightarrow 0}h[\mathit{f}(a)+\mathit{f}(a+h)+\mathit{f}(a+2h)[\mathit{f}(a)\mathit{f}(a+(n-1)h)]]}$$

或者简而言之，$\mathrm{\displaystyle\lim \limits_{h\rightarrow 0}h\displaystyle\sum\limits_{r=0}^{n-1}\mathit{f}(a+r h) }$ 称为 f(x) 关于 x 从 a 到 b 的定积分，用符号表示。

$$\mathrm{\int_{a}^{b}\mathit{f}(x) d x }$$

这里 b 称为积分的上限或上界，a 称为其下限或下界。因此，

$$\mathrm{\int_{a}^{b}\mathit{f}(x) d x =\displaystyle\lim \limits_{h\rightarrow 0}h\displaystyle\sum\limits_{r=0}^{n-1}\mathit{f}(a+r h) }$$

其中 nh=b-a，前提是极限存在。

在数学中，简单的求和和加法很容易，但是当涉及到计算复杂的积分时，简单的计算和加法是不够的，需要积分。在计算定积分时，计算可能很繁琐和复杂，因此使用经验上证明的性质可以使计算相对容易。

曲线下面积的定积分

假设我们想找到由连续曲线 y=x²、x 轴、纵坐标 x=1 和纵坐标 x=4 围成的面积。

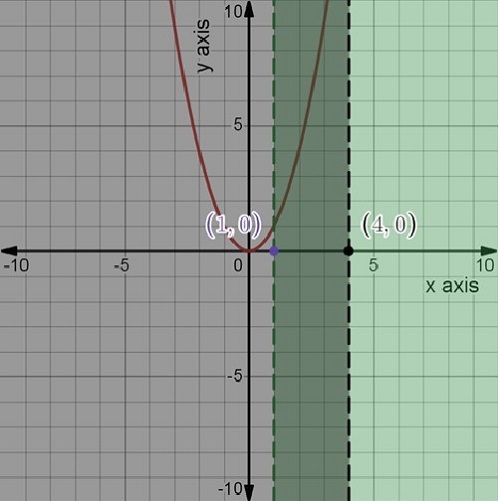
显然，可以通过将区间 1≤x≤4 分成 10 个等长的子区间，用点 x=1, 1.3, 1.6,…划分，并在每个细分点处竖起纵坐标，将该面积分成 10 部分。因此，封闭面积可以表示为 10 项级数的形式。类似地，如果区间 1≤x≤4 被分成 100 个等长的子区间，用点 x=1, 1.03, 1.06,…划分，并在每个细分点处竖起纵坐标，那么封闭面积可以表示为 100 项级数的形式。

定积分的性质

定积分的性质：

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(t) d(t)}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=-\int_{b}^{a}\mathit{f}(x) dx}$

• $\mathrm{\int_{a}^{a}\mathit{f}(x) d x=0}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{c}\mathit{f}(x) d x+\int_{c}^{b}\mathit{f}(x) d x}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(a + b – x) d x}$

• $\mathrm{\int_{0}^{a}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(a – x) d x}$

例题

1. 计算 $\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}}$

因为，

$$\mathrm{\int\frac{dx}{x(1+logx)^2}=-\frac{1}{z}=-\frac{1}{1+logx}}$$

因此，$\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}=-[\frac{1}{1+logx}]_1^e=-[\frac{1}{1+loge}-\frac{1}{1+log1}]=-(\frac{1}{2}-1)=\frac{1}{2}}$

因此， $\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}=\frac{1}{2}}$。

2. 如果 $\mathrm{\mathit{f}(x)=\mathit{f}(a+x)}$，则证明 $\mathrm{\int_a^{a+t} \mathit{f}(x)dx }$ 与 a 无关。

我们令 x=a+z；因此，dx=dz。

同样，当 x=a 时，z=0；当 x=a+t 时，z=t。

因此，

$\mathrm{ \int_a^{a+t} f(x)dx=\int_0^t f(a+z)dz=\int_0^t f(a+x)dx=\int_0^t f(x)dx }$，它与 a 无关。

证毕。

3. 计算以下定积分：$\mathrm{ \int_{-a}^a \frac{dx}{x^a+a^2}}$。

$$\mathrm{\int_{-a}^a \frac{dx}{x^a+a^2}=\frac{1}{a}[tan^{-1} \frac{x}{a}]^a_{-a}=\frac{1}{a}[tan^{-1} \frac{a}{a}-tan^{-1} \frac{-a}{a}]}$$

$$\mathrm{=\frac{1}{a}[tan^{-1} 1-tan^{-1} (-1)]=\frac{1}{a}[\frac{π}{4}-(-\frac{π}{4})]=\frac{π}{2a}}$$

因此，$\mathrm{\int_{-a}^a \frac{ dx}{x^a+a^2}=\frac{π}{2a}}$

结论

积分，顾名思义，用于整合某些东西。在数学中，积分是一种整合函数的方法。积分的另一个术语可以是求和，或者是一种图形化的方式来查找曲线函数下的面积，用于总结整个函数。积分被称为导数的反面，函数分解成更小的函数，积分将较小的部分相加以获得曲线下的总面积。以级数的形式封闭的面积，其项数可以越来越大，每一项的值越来越小。在这种情况下，这样的级数的和的极限值称为定积分。

常见问题

1. 什么是定积分？

定积分定义了曲线下方在两个固定极限之间的面积。这表示为 ∫a.0f (x) dx。其中 a 和 b 分别是定义在 x 轴上的函数 f (x) 的下限和上限。

2. 如何计算定积分？

定积分的计算方法如下：

步骤 1：找到不定积分的积分。

步骤 2：将极限应用于结果

步骤 3：代入上限和下限，然后减去得到的值。

3. 计算特定积分时首先要考虑什么？

要计算定积分，必须首先计算函数的不定积分。因此，计算定积分时首先要考虑的是取定积分并进行积分。

4. 如何用图形方法计算定积分？

定积分的计算是求曲线下方面积。为了找到两个边界之间曲线下方的面积，将面积分成矩形并求和这些面积。矩形越多，面积越精确。因此，将面积分成无限多个大小相同（非常小）的矩形，并将所有面积相加。

5. 如何计算定积分？

定积分可以使用多种方法进行计算。计算定积分的各种方法：

• 基本分析定理

• 用代换法计算定积分

• 用图形法计算定积分

• 用几何法计算定积分

• 用性质计算定积分

6. 定积分的目的是什么？

定积分的一些应用：

• 可以使用定积分来求曲线下方以及两条曲线之间的面积。

• 可以使用定积分来确定 3D 物体的体积。

• 使用定积分计算曲线的弧长。

• 力函数积分也可用于确定功。

• 浸没在液体中的物体所受的力也可以用定积分来计算。