数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会科学
时尚研究
法律研究确定积分的梯形法则
可以使用这个梯形法则解决确定积分。要把函数 f(x) 在范围 a 到 b 之间积分，其实就是找到从 x = a 到 x = b 的曲线下方区域的面积。
要找到那个面积，我们可以把面积分成 n 个梯形，每个梯形的宽度为 h，所以我们可以说 (b - a) = nh。当梯形数量增加时，面积计算的结果会更准确。要解决积分，我们将使用这个公式。
这里的 h 是间隔的宽度，n 是间隔的数量。我们可以使用 计算 h
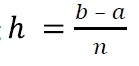
输入和输出
Input: The function f(x): 1-exp(-x/2.0) and limits of the integration: 0, 1. The number of intervals: 20 Output: The answer is: 0.21302
算法
integrateTrapezoidal(a, b, n)
输入： 下限和上限，以及积分数 n。
输出： 积分结果。
Begin h := (b - a)/n sum := f(a) + f(b) for i := 1 to n, do sum := sum + f(a + ih) done return sum End
示例
#include<iostream>
#include<cmath>
using namespace std;
float mathFunc(float x) {
return (1-exp(-x/2.0)); //the function 1 - e^(-x/2)
}
float integrate(float a, float b, int n) {
float h, sum;
int i;
h = (b-a)/n; //calculate the distance between two interval
sum = (mathFunc(a)+mathFunc(b))/2; //initial sum using f(a) and f(b)
for(i = 1; i<n; i++) {
sum += mathFunc(a+i*h);
}
return (h*sum); //The result of integration
}
main() {
float result, lowLim, upLim;
int interval;
cout << "Enter Lower Limit, Upper Limit and interval: "; cin >>lowLim >>upLim >>interval;
result = integrate(lowLim, upLim, interval);
cout << "The answer is: " << result;
}输出
Enter Lower Limit, Upper Limit and interval: 0 1 20 The answer is: 0.21302
更新日期：2020-06-17
1K+ 浏览
广告