数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
时尚研究
法律研究适用于微分方程的龙格-库塔四阶法则
龙格-库塔法用于解决常微分方程 (ODE)。它使用 dy/dx 函数表示 x 和 y，还需要 y 的初始值，即 y(0)。它找到 x 的给定 y 的近似值。为了解决 ODE，我们必须遵循以下公式
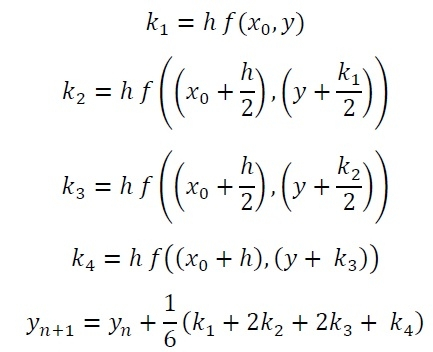
此处 h 为区间高度。
注意：根据这些公式，我们可以使用前两个 k1 和 k2 找到 ODE 的龙格-库塔二阶解。
输入和输出
Input: The x0 and f(x0): 0 and 0 the value of x = 0.4 the value of h = 0.1 Output: Answer of differential equation: 0.0213594
算法
rungeKutta(x0, y0, x, h)
输入 −初始 x 和 y 值、目标 x 值以及区间高度 h。
输出 −值 x 的 y 值。
Begin iteration := (x – x0)/h y = y0 for i := 1 to iteration, do k1 := h*f(x0, y) k2 := h*f((x0 + h/2), (y + k1/2)) k3 := h*f((x0 + h/2), (y + k2/2)) k4 := h*f((x0 + h), (y + k3)) y := y + (1/6)*(k1 + 2k2 + 2k3 + k4) x0 := x0 + h done return y End
示例
#include <iostream>
using namespace std;
double diffOfy(double x, double y) {
return ((x*x)+(y*y)); //function x^2 + y^2
}
double rk4thOrder(double x0, double y0, double x, double h) {
int iteration = int((x - x0)/h); //calculate number of iterations
double k1, k2, k3, k4;
double y = y0; //initially y is f(x0)
for(int i = 1; i<=iteration; i++) {
k1 = h*diffOfy(x0, y);
k2 = h*diffOfy((x0+h/2), (y+k1/2));
k3 = h*diffOfy((x0+h/2), (y+k2/2));
k4 = h*diffOfy((x0+h), (y+k3));
y += double((1.0/6.0)*(k1+2*k2+2*k3+k4)); //update y using del y
x0 += h; //update x0 by h
}
return y; //f(x) value
}
int main() {
double x0, y0, x, h;
cout << "Enter x0 and f(x0): "; cin >> x0 >> y0;
cout << "Enter x: "; cin >> x;
cout << "Enter h: "; cin >> h;
cout << "Answer of differential equation: " << rk4thOrder(x0, y0, x, h);
}输出
Enter x0 and f(x0): 0 0 Enter x: 0.4 Enter h: 0.1 Answer of differential equation: 0.0213594
更新日期：17-6-2020
2,000+ 浏览
广告