LCR 串联电路 - 微分方程与解析解

---

引言

LCR 串联电路有很多应用。在电子学中，元件可以分为两大类：有源元件和无源元件。电阻器、电容器和电感器是一些无源元件。这些元件的组合构成了 RC、RL、LR、LC 和 LCR 电路。RC 电路由电阻器和电容器组成。RL 电路包括电阻器和电感器。在 LR 电路中，电感器和电阻器连接在一起。此外，LC 电路由电感器和电容器组成。LCR 是 L（电感）、C（电容）和 R（电阻）的缩写。LCR 电路由电感器、电容器和电阻器组成。它也可以称为 RLC 电路。

R、L 和 C 在电路中的作用

• 电阻器 - 在电路中，电阻器用 R 表示。通常，能量以热的形式衰减。对于流过它的恒定电流，将存在恒定的电压降。

• 电感器 - 电感器用 L 表示。能量以磁场的形式存储。它会阻止电流的变化。它由线圈绕组线组成。

• 电容器 - 电容器用 C 表示。它类似于电感器。它以电场的形式存储能量。它也阻止电流变化。

什么是 LCR 电路？

LCR 电路是由电感器、电容器和电阻器串联或并联连接而成的电路。在串联 LCR 电路中，电阻器、电感器和电容器与输入源串联。输入源 Vs 是所有三个元件（即电阻器、电容器和电感器）的相量和。电流对于所有三个元件都是相同的。

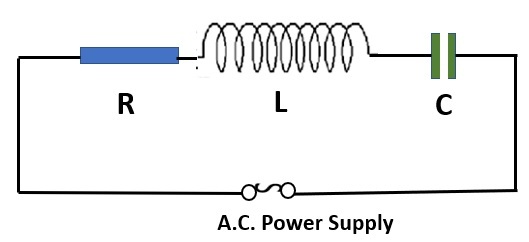
串联 LCR 电路的阻抗

考虑电阻 R、电感 L 和电容 C 上的电压幅度分别为 𝑽_𝑹、𝑽_𝑳 和 𝑽_𝑪。

因为，𝑉_𝑹 = 𝑖𝑅

其中 i 是电流，R 是电阻

$$\mathrm{V_L=iX_L=i\omega L}$$

其中 X_L 是感抗，ω 是角频率，L 是电感 $\mathrm{V_C=iX_C=i(\frac{1}{\omega C})}$

其中 X_C 是容抗，C 是电容

$$\mathrm{We\: have\: V^2=V_R^2+(V_L-V_C )^2}$$

代入后得到：

$$\mathrm{V^2=(iR)^2+(iX_L-iX_C )^2}$$

$$\mathrm{V^2=i^2 (R^2+(X_L-X_C )^2 )}$$

则电流：

$$\mathrm{ i=\frac{v}{\sqrt{(R^2+(X_L-X_C )^2)}}=\frac{v}{Z}}$$

其中 Z 是阻抗

$$\mathrm{Z=\sqrt{(R^2+(X_L-X_C )^2)}}$$

代入感抗和容抗的值：

LCR 电路的阻抗 (Z)：

$$\mathrm{Z=\sqrt{R^2+\lbrace \omega L-\frac{1}{\omega C}\rbrace^2}}$$

LCR 电路推导、LCR 电路的谐振和解析解

假设电阻器、电感器和电容器与输入源串联。交流输入由下式给出：

$$\mathrm{v=v_m sin\omega t}$$

其中 ω 是角频率，v_m 是输入源的幅度，“t”是时间

使用基尔霍夫定律：

$$\mathrm{L\frac{\text{d}i}{\text{d}t}+iR+\frac{q}{C}=v …. (1)}$$

其中 L 是电感，i 是电流，R 是电阻，q 是电荷，C 是电容 分析电路：

$$\mathrm{i=\frac{\text{d}q}{\text{d}t}……………… … (2)}$$

对式 (2) 求导，我们有

$$\mathrm{\frac{\text{d}i}{\text{d}t}=\frac{\text{d}^2q}{\text{d}t^2} …. (3) }$$

将式 (2) 和 (3) 代入式 (1)：

$$\mathrm{L \frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+q/C=v_m sin\omega t …. (4)}$$

对于阻尼振荡器方程，上述方程是类似的。

$$\mathrm{q=q_m sin(\omega t+ θ)}$$

$$\mathrm{\frac{\text{d}q}{\text{d}t}=q_m \omega cos(\omega t+ θ)}$$

$$\mathrm{\frac{\text{d}^2q}{\text{d}t2}=-q_m \omega ^2 sin(\omega t+ θ)}$$

将上述方程代入电压方程：

$$\mathrm{q_m \omega [Rcos(\omega t+ θ)+(X_C-X_L )sin(\omega t+ θ)]=v_m sin\omega t}$$

我们知道容抗 $\mathrm{X_C=\frac{1}{\omega C}}$ 和感抗 $\mathrm{X_L=\omega L}$

此外，LCR 电路的阻抗 (Z)：

$$\mathrm{ Z=\sqrt{(R^2+(X_L-X_C )^2 )}}$$

代入后得到值：

$$\mathrm{\frac{q_m \omega}{Z} [\frac{R}{Z} cos(\omega t+ θ)+(\frac{(X_C-X_L)}{Z})sin(\omega t+ θ)]}$$

求解 θ 和 ϕ 的方程，得到 LCR 电路中电流的方程：

$$\mathrm{i=\frac{\text{d}q}{\text{d}t}=q_m \omega cos(\omega t+ θ)=i_m \omega cos(\omega t+ θ)}$$

$$\mathrm{i=i_m sin(\omega t+ ϕ) }$$

电谐振 -

谐振的过程在具有在特定频率下振荡趋势的不同系统中非常常见。此频率称为系统的固有振荡频率。在 LCR 系统中，此频率由电感、电容和电阻的值决定。

结论

在电子学中，元件可以分为两大类：有源元件和无源元件。电阻器、电容器和电感器是一些无源元件。这些无源元件的组合构成了 RC、RL、LR、LC 和 LCR 电路。LCR 电路是由电感器、电容器和电阻器串联或并联连接而成的电路。LCR 电路的阻抗 (Z)

$$\mathrm{Z=\sqrt{R^2+\lbrace \omega L-\frac{1}{\omega C}\rbrace^2}}$$

在找到解析解后，得到 LCR 电路中电流的方程：

$$\mathrm{i=\frac{\text{d}q}{\text{d}t}=q_m \omega cos(\omega t+ θ)=i_m \omega cos(\omega t+ θ)=i_m sin(\omega t+ ϕ)}$$

常见问题

1. 描述谐振频率。

当系统的振荡频率等于其固有频率时，称为谐振频率。

2. 电感器、电阻器和电容器的共同点是什么？

这些器件是双端线性器件。这些器件随着施加电压的增加，线性地通过电路传输电流。

3. 电感器在 LCR 电路中的重要性是什么？

只有施加电流时，电感器才能储存磁能。电感器以磁场的形式保持加速电子的动态能量。

4. LCR 电路的重要性是什么？

LCR 电路由于以下原因很有用：

• LCR 电路通过控制流经元件的电流来帮助减少功耗，从而防止过热。

• 它还有助于减少电压波动，从而防止损坏电子设备。

• LCR 电路有助于储存能量并以受控方式释放能量，这将有助于防止电流流过电阻器。

5. 串联谐振 LCR 电路如何在电视中使用？

该应用可以在收音机和电视接收机上显示。收音机/电视的天线拦截来自许多广播电台的信号。如果我们想接收特定的电台/电视台，我们可以通过改变调谐电路中电容器的电容来调谐接收机，从而使电路的谐振频率等于该特定电台的频率。