利用拉普拉斯变换分析串联RLC电路的阶跃响应

拉普拉斯变换

拉普拉斯变换是一种数学工具，用于将时域中的微分方程转换为频域或s域中的代数方程。

数学上，如果$\mathrm{\mathit{x\left ( t \right )}}$是时域函数，则其拉普拉斯变换定义为：

$$\mathrm{\mathit{L\left [ x\left ( t \right ) \right ]\mathrm{\mathrm{=}}X\left ( s \right )\mathrm{\mathrm{=}}\int_{-\infty }^{\infty }x\left ( t \right )e^{-st}\; dt\; \; \; \cdot \cdot \cdot \left ( \mathrm{1} \right )}}$$

此外，该函数的拉普拉斯逆变换定义为：

$$\mathrm{\mathit{L^{-\mathrm{1}}\left [X\left ( s \right ) \right ]\mathrm{\mathrm{=}}x\left ( t \right ) \mathrm{\mathrm{=}}\int_{\sigma -j\infty }^{\sigma \mathrm{\: +\: }j\infty }X\left ( s \right )e^{st}\; ds\; \; \; \cdot \cdot \cdot \left ( \mathrm{2} \right )}}$$

串联RLC电路的阶跃响应

串联RLC电路如图1所示。

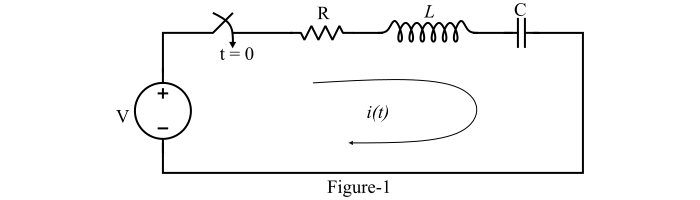
描述该系统的方程为：

$$\mathrm{\mathit{Vu\left ( t \right )\mathrm{\mathrm{=}}Ri\left ( t \right )\mathrm{\: +\: }L\frac{di\left ( t \right )}{dt}\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{t}i\left ( t \right )dt}}$$

$$\mathrm{\Rightarrow \mathit{Vu\left ( t \right )\mathrm{\mathrm{=}}Ri\left ( t \right )\mathrm{\: +\: }L\frac{di\left ( t \right )}{dt}\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{-\infty }^{\mathrm{0}}i\left ( t \right )dt\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt\; \; \cdot \cdot \cdot \left ( \mathrm{3} \right )}}$$

在等式(3)两侧进行拉普拉斯变换，得到：

$$\mathrm{\mathit{\mathrm{\textbf{L}}\left [ Vu\left ( t \right ) \right ]\mathrm{\mathrm{=}}\mathrm{\textbf{L}}\left [ Ri\left ( t \right ) \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ L\frac{di\left ( t \right )}{dt} \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ \frac{\mathrm{1}}{C}\int_{-\infty }^{\mathrm{0}}i\left ( t \right )dt \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ \frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt \right ]}}$$

$$\mathrm{\mathit{\Rightarrow \frac{V}{s}\mathrm{=}RI\left ( s \right )\mathrm{\: +\: }L\left [ sI\left ( s \right )-i\left ( \mathrm{0^{\mathrm{\: +\: }}} \right ) \right ]\mathrm{\: +\: }\frac{\mathrm{1}}{C}\mathrm{\textbf{L}}\left [ q\left ( \mathrm{0^{\mathrm{\: +\: }}} \right ) \right ]\mathrm{\: +\: }\frac{\mathrm{1}}{C}\frac{I\left ( s \right )}{s}\; \; \cdot \cdot \cdot \left ( \mathrm{4} \right )}}$$

其中：

• $\mathrm{\mathit{i\left ( \mathrm{0}^{\mathrm{ + }} \right )}}$是电感器中的初始电流，

• $\mathrm{\mathit{q\left ( \mathrm{0}^{\mathrm{ + }} \right )}}$是电容器上的初始电荷。

忽略电感器和电容器的初始条件，我们可以将等式(4)写成：

$$\mathrm{\mathit{\frac{V}{s}\mathrm{\mathrm{=}}RI\left ( s \right )\mathrm{\: +\: }LsI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{1}}{C}\frac{I\left ( s \right )}{s}}}$$

$$\mathrm{\Rightarrow \mathit{\frac{V}{s}\mathrm{\mathrm{=}}\left ( R\mathrm{\: +\: }sL\mathrm{\: +\: }\frac{\mathrm{1}}{sC} \right )I\left ( s \right )\; \; \cdot \cdot \cdot \left ( \mathrm{5} \right )}}$$

因此，电路中的电流由下式给出：

$$\mathrm{ \mathit{I\left ( s \right )\mathrm{\mathrm{=}}\frac{V}{\left ( sR\mathrm{\: +\: }s^{\mathrm{2}}L\mathrm{\: +\: }\frac{\mathrm{1}}{C} \right )}\; \; \cdot \cdot \cdot \left ( \mathrm{6} \right )}}$$

此外：

$$\mathrm{ \mathit{I\left ( s \right )\mathrm{\mathrm{=}}\frac{V}{L\left [ s^{\mathrm{2}}\mathrm{\: +\: }\left ( \frac{R}{L} \right )s\mathrm{\: +\: }\frac{\mathrm{1}}{LC} \right ]}\mathrm{=}\frac{V}{L\left ( s-a_{\mathrm{1}} \right )\left ( s-a_{\mathrm{2}} \right )}\; \; \cdot \cdot \cdot \left ( \mathrm{7} \right )}}$$

其中，$\mathrm{\mathit{a_{\mathrm{1}}}}$和$\mathrm{\mathit{a_{\mathrm{2}}}}$是方程$\mathrm{ \mathit{\left [ s^{\mathrm{2}}\mathrm{\: +\: }\left ( \frac{R}{L} \right )s\mathrm{\: +\: }\frac{\mathrm{1}}{LC} \right ]}}$的根，由下式给出：

$$\mathrm{ \mathit{a_{\mathrm{1}},a_{\mathrm{2}}\mathrm{=}-\frac{R}{\mathrm{2}L}\pm\frac{\mathrm{1}}{\mathrm{2}L}\sqrt{R^{\mathrm{2}}-\frac{\mathrm{4}L}{C}}\; \; \cdot \cdot \cdot \left ( \mathrm{8} \right )}}$$

现在，通过对等式(8)进行拉普拉斯逆变换，我们可以得到电流作为时间函数，即：

$$\mathrm{ \mathit{i\left ( t \right )\mathrm{=}L^{-\mathrm{1}}\left [ I\left ( s \right ) \right ]\mathrm{=}L^{-\mathrm{1}}\left [ \frac{V}{L\left ( s-a_{\mathrm{1}} \right )\left ( s-a_{\mathrm{2}} \right )} \right ] }}$$

$$\mathrm{ \mathit{i\left ( t \right )\mathrm{=}\frac{V}{L\left ( a_{\mathrm{1}}-a_{\mathrm{2}} \right )}\left [ e^{a_{\mathrm{1}}t} - e^{a_{\mathrm{2}}t}\right ]\; \; \cdot \cdot \cdot \left ( \mathrm{9} \right )}}$$

等式(9)是串联RLC电路的阶跃响应。

数值示例

求图2所示串联RLC电路中的电流。

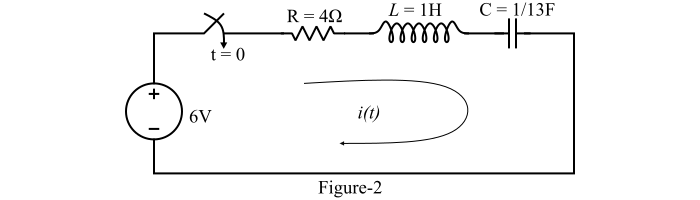
解决方案

描述给定串联RLC电路的KVL方程为：

$$\mathrm{\mathit{\mathrm{6}u\left ( t \right )\mathrm{\mathrm{=}}Ri\left ( t \right )\mathrm{\: +\: }L\frac{di\left ( t \right )}{dt}\mathrm{\: +\: }\frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt}}$$

在上述方程两侧进行拉普拉斯变换，得到：

$$\mathrm{\mathit{\mathrm{\textbf{L}}\left [ \mathrm{6}u\left ( t \right ) \right ]\mathrm{\mathrm{=}}\mathrm{\textbf{L}}\left [ Ri\left ( t \right ) \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ L\frac{di\left ( t \right )}{dt} \right ]\mathrm{\: +\: }\mathrm{\textbf{L}}\left [ \frac{\mathrm{1}}{C}\int_{\mathrm{0} }^{t}i\left ( t \right )dt \right ]}}$$

$$\mathrm{\Rightarrow \mathit{\frac{\mathrm{6}}{s}\mathrm{\mathrm{=}}RI\left ( s \right )\mathrm{\: +\: }sLI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{1}}{sC}I\left ( s \right )}}$$

代入R，L和C的值，得到：

$$\mathrm{\mathit{\frac{\mathrm{6}}{s}\mathrm{\mathrm{=}}\mathrm{4}I\left ( s \right )\mathrm{\: +\: }sI\left ( s \right )\mathrm{\: +\: }\frac{\mathrm{13}}{s}I\left ( s \right )}}$$

$$\mathrm{\Rightarrow \mathit{\left ( s^{\mathrm{2}}\mathrm{\: +\: }\mathrm{4}s\mathrm{\: +\: }\mathrm{13} \right )I\left ( s \right )\mathrm{=}\mathrm{6}}}$$

$$\mathrm{\therefore \mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{6}}{\left ( s^{\mathrm{2}}\mathrm{\: +\: }\mathrm{4}s\mathrm{\: +\: }\mathrm{13} \right )}\mathrm{=}\frac{\mathrm{6}}{\left ( s\mathrm{\: +\: 2} \right )^{\mathrm{2}}\mathrm{\: +\: }\mathrm{3^{2}}}}}$$

$$\mathrm{\Rightarrow \mathit{I\left ( s \right )\mathrm{=}\frac{\mathrm{6}}{\mathrm{3}}\left [ \frac{\mathrm{3}}{\left ( s\mathrm{\: \mathrm{\: +\: } \: 2} \right )^{\mathrm{2}}\mathrm{\: +\: }\mathrm{3^{2}}} \right ]}}$$

进行拉普拉斯逆变换，得到：

$$\mathrm{ \mathit{i\left ( t \right )\mathrm{=}L^{-\mathrm{1}}\left [ I\left ( s \right ) \right ]\mathrm{=}\frac{\mathrm{6}}{\mathrm{3}}L^{-\mathrm{1}}\left [ \frac{\mathrm{3}}{\left ( s\mathrm{\: \mathrm{\: +\: } \: 2} \right )^{\mathrm{2}}\mathrm{\: +\: }\mathrm{3^{2}}} \right ]}}$$

$$\mathrm{ \therefore \mathit{i\left ( t \right )\mathrm{=}\mathrm{2}e^{-\mathrm{2}t}\: \mathrm{sin\, 3}t\: u\left ( t \right )}}$$

Manish Kumar Saini

更新于： 2022年1月5日

14K+ 次查看

启动您的职业生涯

通过完成课程获得认证

开始学习