数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律利用拉普拉斯变换分析串联RL电路的阶跃响应和冲激响应
图1所示为一个由电阻(R)和电感(L)串联组成的电路。假设开关(S)在时间t=0时闭合。
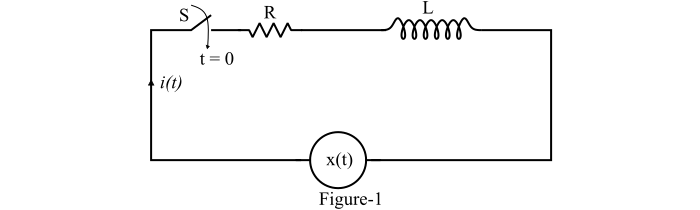
串联RL电路的阶跃响应
为了得到串联RL电路的阶跃响应，施加到电路的输入x(t)由下式给出：
x(t)=Vu(t)
现在，根据基尔霍夫电压定律(KVL)，我们得到以下微分方程：
Vu(t)=Ri(t)+Ldi(t)dt
对两边进行拉普拉斯变换，得到：
Vs=RI(s)+L[sI(s)−i(0−)]
电感中的电流不能突变。因此，在t=0之前，电路中的电流为零，即电感中的初始电流为i(0−)=0。于是：
Vs=RI(s)+sLI(s)
⇒Vs=(R+sL)I(s)
因此，电路电流由下式给出：
⇒I(s)=Vs(R+sL)
⇒I(s)=VL[1s(s+RL)]=VL⋅LR[1s−1(s+RL)]
⇒I(s)=VR[1s−1(s+RL)]
对上述方程进行拉普拉斯反变换，得到：
i(t)=VR[1−e−(R/L)t]
这就是串联RL电路的阶跃响应。
串联RL电路的冲激响应
为了得到串联RL电路(图1所示)的冲激响应，施加到电路的输入x(t)由下式给出：
x(t)=δ(t)
根据KVL，得到电路的以下微分方程：
δ(t)=Ri(t)+Ldi(t)dt
对两边进行拉普拉斯变换，得到：
L[δ(t)]=L[Ri(t)]+L[Ldi(t)dt]
(L为拉普拉斯变换算子，L为电感的电感量)
⇒1=RI(s)+L[sI(s)−i(0−)]
忽略初始条件，即i(0−)=0。则：
(R+sL)I(s)=1
因此，对于冲激输入，RL串联电路中的电流为：
I(s)=1(R+sL)=1L(s+RL)
进行拉普拉斯反变换，得到：
L−1[I(s)]=L−1[1L(s+RL)]
∴
这就是串联RL电路的冲激响应。
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
数值示例
求图2所示串联RL电路的阶跃响应和冲激响应。
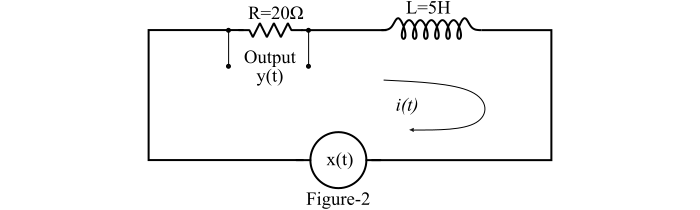
解答
描述图2所示串联RL电路的微分方程为：
\mathrm{\mathit{x\left ( t \right )\mathrm{=}\mathrm{20}i\left ( t \right )\mathrm{+}\mathrm{5}\frac{di\left ( t \right )}{dt}}}
对两边进行拉普拉斯反变换，得到：
\mathrm{\mathit{X\left ( s \right )\mathrm{=}\mathrm{20}I\left ( s \right )\mathrm{+}\mathrm{5}\left [ sI\left ( s \right )-i\left ( \mathrm{0}^{-} \right ) \right ]}}
忽略电路的初始条件，得到：
\mathrm{\mathit{X\left ( s \right )\mathrm{=}\mathrm{20}I\left ( s \right )\mathrm{\: +\: }\mathrm{5} sI\left ( s \right )\mathrm{=}\mathrm{5}I\left ( s \right )\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}
\mathrm{\mathit{\therefore I\left ( s \right )\mathrm{=}\frac{X\left ( s \right )}{\mathrm{5}\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}}
参考图2的电路，电路的输出为：
\mathrm{\mathit{Y\left ( s \right )\mathrm{=}\mathrm{20}I\left ( s \right )\mathrm{=}\mathrm{20}\left [ \frac{X\left ( s \right )}{\mathrm{5}\left ( s\mathrm{\: +\: }\mathrm{4} \right )} \right ]}}
\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{=}\left [ \frac{\mathrm{4}}{\left ( s\mathrm{\: +\: }\mathrm{4} \right )} \right ]X\left ( s \right )}}
对于单位阶跃响应
\mathrm{输入,\mathit{x\left ( t \right )\mathrm{=}u\left ( t \right )}}
\mathrm{\mathit{\therefore X\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{s}}}
因此，电路的输出为：
\mathrm{\mathit{Y\left ( s \right )\mathrm{=}\left [ \frac{\mathrm{4}}{\left ( s\mathrm{\: +\: }\mathrm{4} \right )} \right ]\left ( \frac{\mathrm{1}}{s} \right )\mathrm{=}\frac{\mathrm{4}}{s\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}}
\mathrm{\mathit{\Rightarrow Y\left ( s \right )\mathrm{=}\frac{\mathrm{1}}{s}-\frac{\mathrm{1}}{\left ( s\mathrm{\: +\: }\mathrm{4} \right )}}}
进行拉普拉斯反变换，电路的阶跃响应由下式给出：
\mathrm{\mathit{L^{-\mathrm{1}}\left [ Y\left ( s \right ) \right ]\mathrm{=}L^{-\mathrm{1}}\left [ \frac{\mathrm{1}}{s} \right ]-L^{-\mathrm{1}}\left [ \frac{\mathrm{1}}{\left ( s\mathrm{\, +\,}\mathrm{4} \right )} \right ]}}
\mathrm{\mathit{\Rightarrow y\left ( t \right )\mathrm{=}u\left ( t \right )-e^{-\mathrm{4}t}u\left ( t \right )}}
\mathrm{\mathit{\therefore y\left ( t \right )\mathrm{=}u\left ( t \right )\left [\mathrm{1} -e^{-\mathrm{4}t} \right ]}}
对于冲激响应
\mathrm{\mathit{x\left ( t \right )\mathrm{=}\delta \left ( t \right )}}
\mathrm{\mathit{\therefore X\left ( s \right )\mathrm{=}\mathrm{1}}}
\mathrm{输出,\mathit{ Y\left ( s \right )\mathrm{=}\left [ \frac{\mathrm{4}}{\left ( s\mathrm{\, +\,}\mathrm{4} \right )} \right ]\left ( \mathrm{1} \right )\mathrm{=}\frac{\mathrm{4}}{\left ( s\mathrm{\, +\,}\mathrm{4} \right )}}}
进行拉普拉斯反变换，电路的冲激响应由下式给出：
\mathrm{\mathit{ y\left ( t \right )\mathrm{=}\mathrm{4}e^{-\mathrm{4}t}u\left ( t \right )}}
10K+ 浏览量
