利用拉普拉斯变换进行电路分析

拉普拉斯变换

拉普拉斯变换是一种数学工具，用于将时域中的微分方程转换为频域或s域中的代数方程。

数学上，如果$\mathrm{\mathit{x\left(t\right)}}$是时域函数，则其拉普拉斯变换定义为：

$$\mathrm{\mathit{L\left[\mathit{x}\mathrm{\left(\mathit{t} \right )}\right ]\mathrm{=}X\mathrm{\left ( \mathit{s}\right)}\mathrm{=}\int_{-\infty }^{\infty}x\mathrm{\left (\mathit{t} \right )}e^{-st} \:dt}}$$

利用拉普拉斯变换进行电路分析

拉普拉斯变换可以用来解决不同的电路问题。为了解决电路问题，首先需要写出电路的微分方程，然后利用拉普拉斯变换求解这些微分方程。此外，电路本身也可以使用拉普拉斯变换转换为s域，然后写出并求解对应的电路代数方程。

电路可以包含三种电路元件：电阻器(R)、电感器(L)和电容器(C)，下面将讨论使用拉普拉斯变换分析这些元件的方法。

纯电阻电路

图1显示了一个由纯电阻元件组成的电路。

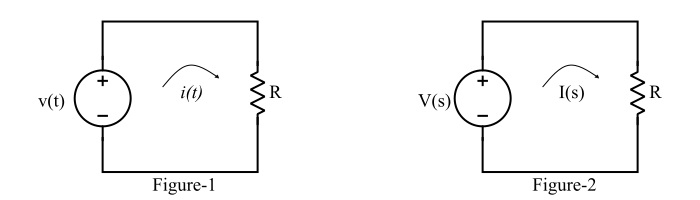
通过在这个电路中应用基尔霍夫电压定律(KVL)，我们可以写出：

$$\mathrm{\mathit{v\mathrm{\left(\mathit{t}\right )}\mathrm{=}Ri\mathrm{\left ( \mathit{t}\right)}}}$$

因此，该方程的拉普拉斯变换为：

$$\mathrm{\mathit{V\mathrm{\left(\mathit{s}\right )}\mathrm{=}RI\mathrm{\left ( \mathit{s}\right)}}}$$

这里需要注意的是，时域中的电阻R在s域中仍然是R。该电路的拉普拉斯变换版本如图2所示。

纯电感电路

图3显示了一个由纯电感器组成的电路。

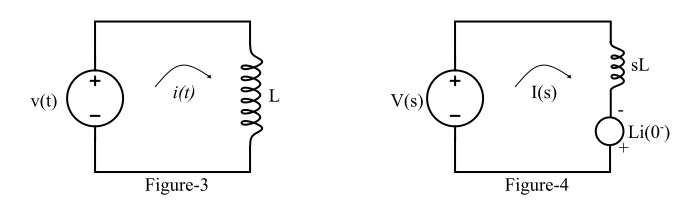
纯电感元件的电压方程为：

$$\mathrm{\mathit{v\mathrm{\left(\mathit{t}\right)}\mathrm{=} L\frac{di\mathrm{\left(\mathit{t} \right )}}{dt}}}$$

对等式两边进行拉普拉斯变换，得到：

$$\mathrm{\mathit{V\mathrm{\left(\mathit{s}\right)}\mathrm{=} \mathrm{\left[\mathit{sI}\mathrm{\left (\mathit{s} \right)}-\mathit{i\mathrm{\left (0^{-} \right )}}\right]}L}}$$

$$\mathrm{\Rightarrow \mathit{V\mathrm{\left(\mathit{s}\right)}\mathrm{=} sLI\mathrm{\left ( \mathit{s}\right)-\mathit{Li}\mathrm{\left ( 0^{-}\right )}}}}$$

其中，$i\mathrm{\left ( 0^{-}\right )}$是流过电感的初始电流。

时域中元件的电感($\mathit{L}$)在s域中变为sL。此外，电路电流$I\mathrm{\left(\mathit{s}\right)}$受到电压$Li\mathrm{\left(\mathrm{0^{-}}\right)}$的阻碍。纯电感电路的拉普拉斯变换版本如图4所示。

纯电容电路

图5显示了一个由纯电容元件组成的电路。

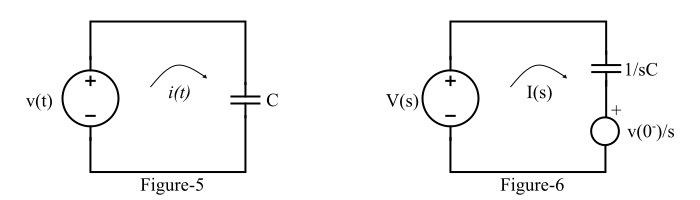
流过电容器的电流为：

$$\mathrm{\mathit{i}\mathrm{\left(\mathit{t}\right)}\mathrm{=}\mathit{C\:\frac{dv\left(t\right )}{dt}}}$$

对该方程进行拉普拉斯变换，得到：

$$\mathrm{\mathit{I}\mathrm{\left(\mathit{s}\right)}\:\mathrm{=}\:\mathit{C}\mathrm{\left[ \mathit{sV\mathrm{\left(s\right)-\mathit{v}\mathrm{\left ( 0^{-} \right )}}}\right ]}\mathrm{=}sCV\mathrm{\left ( s \right )-\mathit{Cv}\mathrm{\left ( 0^{-} \right )}}}$$

$$\mathrm{\therefore \mathit{I}\mathrm{\left(\mathit{s}\right)}\:\mathrm{=}\:sCV\mathrm{\left ( \mathit{s} \right )-\mathit{q}\mathrm{\left ( 0^{-} \right )}}}$$

同时

$$\mathrm{\mathit{V\mathrm{\left ( \mathit{s} \right )}\mathrm{=}\frac{\mathrm{1}}{\mathit{sC}}I\mathrm{\mathit{\left (s\right )}}}+\frac{\mathrm{1}}{\mathit{sC}}\mathit{q}\mathrm{\mathit{\left (\mathrm{0^{-}}\right )}}}$$

$$\mathrm{\therefore \mathit{V\mathrm{\left ( \mathit{s} \right )}\mathrm{=}\frac{I\mathrm{\left (\mathit{s} \right)}}{sC}\mathrm{+}\frac{v\mathrm{\left(\mathrm{0^{-}} \right )}}{s}}}$$

其中，$\mathrm{\mathit{v\mathrm{\left ( 0^{-} \right )}}}$是电容器两端的初始电压。

很明显，时域中的电容(C)在s域中变为$\mathrm{\left(\frac{1}{\mathit{sc}}\right )}$。此外，在s域中引入了电压$\mathrm{\left [\frac{\mathit{v}\mathrm{\left ( 0^{-} \right )}}{\mathit{s}} \right ]}$，它阻碍了电路电流的流动。纯电容电路的拉普拉斯变换版本如图6所示。

Saini Manish Kumar

更新于：2022年1月3日

19K+ 浏览量

开启您的职业生涯

完成课程获得认证

开始学习