心理学中正态概率分布技术的应用
“正态”一词的字面意思是平均。在心理学研究、社会学研究和教学中,那些在资格和特征方面能够达到特定固定水平的人被称为正态。同时,那些高于或低于这个点的人是非正态的。大自然已经足够慷慨地将大多数属性(如体重、身高、智力等)分配得相当均匀。因此,我们大多数人拥有平均体重、身高、智力和此类属性。相当一部分人明显偏离平均水平,无论高于或低于。这同样适用于从随机选择的样本或人群中通过考试、调查和心理学、社会学和教育实验收集的信息,关于成绩分数、智商分数、评分分数等。如果将这种分布绘制在图表纸上,就会形成一条有趣的典型曲线,类似于钟形的垂直横截面。这种钟形曲线称为正态曲线。
拉普拉斯和高斯(1777-1855)独立推导出了这条曲线。他们研究了物理学和天文学中的实验误差。他们发现结果误差分布是正态的——因此,误差曲线被称为正态误差曲线或仅仅是误差曲线。
什么是正态概率分布?
根据概率原理,它给出了连续变量的可能得分分布。一位名叫亚伯拉罕·棣莫弗的数学家发展了这条曲线,它具有单边的钟形,具有双侧对称性,并且建立在概率原理的基础上。概率的根本原理建立在事件发生的可能性上,正态曲线描绘了这一原理。
计算
将连续变量得分(X)的频率(f)绘制在一个相当大的样本中观察到的频率,相对于其对应的得分(X),得到正态分布曲线。
如果将相对频率(fln)(通过将每个观察到的频率除以总频率n获得)绘制在其对应的标准分数(z分数)上,则可以得到类似形状的分布,这些标准分数是从原始X分数计算得出的,因为z分数是X分数的线性变换;然而,这种分布被称为正态分布,因为它的Y纵坐标提供了Z分数的相对频率或概率,以及伴随的X分数,而不是观察到的频率。
描述正态概率分布的通用数学方程如下所示
$\mathrm{y = \frac{n}{\sigma\sqrt{2\Pi}}e^\frac{−x^{2}}{2\sigma^{2}}}$
其中,
$\mathrm{y}$ = 频率
$\mathrm{n}$ = 观察次数
$\mathrm{\sigma}$ = 分布的标准差
$\mathrm{\Pi}$ = 3.1416(约)
$\mathrm{e}$ = 2.718(约),奈皮尔对数的底数
$\mathrm{x}$ = 测量值与平均值的偏差
示例
样本量为1000例。测试分数的平均值为14.5,标准差为2.5。假设分布为正态,计算12-16分数段中个体的数量。
解答
原始分数12和16都需要转换为z分数。
原始分数12对应的z分数 = $\mathrm{\frac{X − M}{\sigma}}$
= (12−14.5)/2.5
= −2.5/2.5 = −1$\sigma$
原始分数16对应的z分数 = (16 − 14.5)/2.5 = 1.5/2.5
= 0.6 $\sigma$
根据正态曲线表,2257(10000中的),即22.57%的案例位于平均值和0.6 $\sigma$之间。类似地,在−1 $\sigma$和平均值之间,有3413,即34.13%的案例。这样,可以很容易地得出结论,在1000人中,有22.57 + 34.13 = 56.7%或567人的分数在12-16范围内。
性质
正态概率曲线是双侧对称的。正态曲线围绕称为纵坐标的垂直轴双侧对称。50%的曲线位于最大中心纵坐标的左侧,另外50%位于右侧。关于曲线中心点处的纵坐标的对称性表明,曲线一侧的曲线斜率、形状和大小与另一侧相同。下图显示了中心中间点的左右两半。
平均数 = 中位数 = 众数
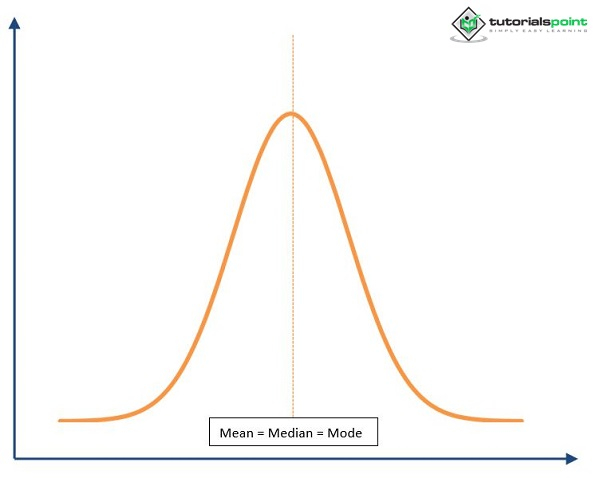
正态概率曲线是单峰的。曲线只有一个顶点,使其成为单峰的,并且只能有一个众数。
最大纵坐标位于中心附近。纵坐标的高度始终在曲线的中心或中点达到峰值,在单位正态曲线上等于0.3989。
正态概率曲线渐近于X轴。曲线的高度在远离中点两端的逐渐减小,渐近地接近X轴,但永远不会接触X轴。因此,它的末端延伸到负无穷大($− \infty$)和正无穷大($+ \infty$)。
曲线高度均匀下降。从顶点向任一方向,曲线的高度都对称下降。
拐点出现在±1个标准差($\pm \: 1 \: \sigma$)处。正态曲线方向从凸到凹的变化发生在一个称为拐点的地方。从两个拐点垂直绘制到X轴的线在平均值上下一个标准差单位的距离处接触中心点。
正态曲线总面积在两个拐点内的百分比是固定的。大约68.26%的总面积位于平均值±1个标准差($\pm$ 1 $\sigma$)单位的范围内。
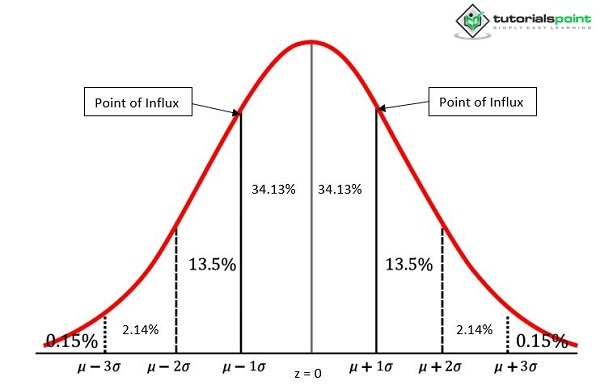
曲线覆盖的总面积也可以接近100%的概率。曲线下的总面积可以认为接近100%的概率,用标准差来解释。
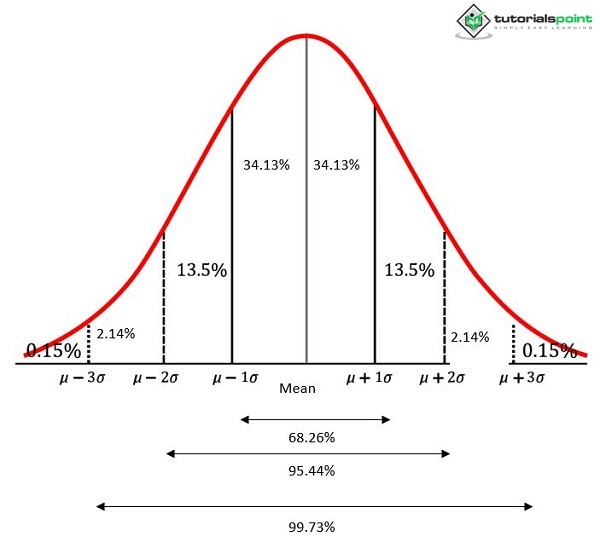
正态分布中连续标准差之间护理的百分比。正态分布作为峰度的基准。它具有中峰特征——其峰度百分位系数为0.263。
正态性偏差
当测试分数的频率分布以直方图或多边形的方式图形化地描绘时,人们很容易注意到曲线形状的对称性或不对称性。三个参数——平均数、中位数和众数——在正态曲线模型中重合;曲线的左右两半完全平衡。通常,正态曲线中会出现两种类型的偏差——峰度和偏度。
结论
正态概率曲线具有很重要的意义。它被广泛应用于心理学、社会学和教育测量。它可以作为计算百分位数和百分位数排名、理解和应用标准测量误差的概念以及转换和组合定性数据的模型。正态概率分布具有可以解决问题的应用,例如将原始分数转换为z分数,并显示正态曲线总面积相对于sigma距离的分数部分。


 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP