使用Python展示统计学中的幂对数正态分布

---

在这篇文章中，我们将学习幂对数正态分布、其应用和用途。我们将学习如何通过包括PDF和CDF在内的不同方法来分析该分布。在此之前，让我们看看什么是幂正态分布。

幂对数正态分布

幂对数正态分布是对数正态分布的一种变体。唯一的区别是，我们通过对对数正态分布应用幂变换来获得幂对数正态分布。幂正态分布和幂对数正态分布的区别在于，幂正态分布是正态分布的变体，而幂对数正态分布是对数正态分布的变体。两者都具有可以定义分布形状的幂参数。

让我们使用各种方法来查看幂对数正态分布：

方法一：随机数生成

在此方法中，我们将从幂对数正态分布生成随机数。为了生成随机数，我们使用scipy.stats模块。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt

c, s = 2.14, 0.446

x = 0.5
random_numbers = powerlognorm.rvs(c, s, size=1000)
plt.hist(random_numbers, bins=30, density=True, alpha=0.5)
plt.xlabel('Values')
plt.ylabel('Probability')
plt.title('Power Log-Normal Distribution')
plt.show()

输出

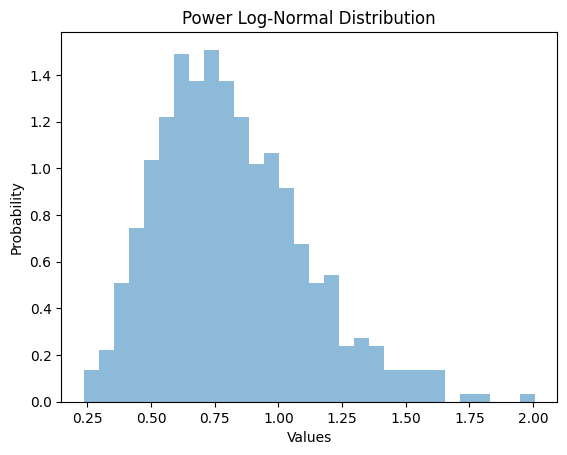
解释

在此方法中，我们从scipy.stats导入powerlognorm类。这里，我们把c, s作为位置参数和形状参数。使用powerlognorm.rvs()，我们从幂对数正态分布生成了1000个随机值，并为这些随机值绘制了直方图。

在函数中，我们从scipy.stats模块导入了powerlognorm类，用于处理幂对数正态分布。这里c是位置参数，s是形状参数。为了计算任何给定点的PDF，我们使用pdf()函数。

方法二：概率密度函数 (PDF)

幂对数正态分布PDF观察特定值的概率。它用于定义任何随机变量的概率。为了分析任何特定点的PDF，我们将使用pdf()方法。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt
c, s = 2.14, 0.446

x = 1.5
pdf_ = powerlognorm.pdf(x, c, s)

print(pdf_)

输出

0.12076527710927452

解释

在此函数中，我们从scipy.stats模块导入**powerlognorm**类。我们使用pdf()函数计算PDF，并将位置和形状参数传递给pdf函数。

方法三：累积分布函数 (CDF)

在此方法中，我们将使用累积分布函数的PDF来描述小于或等于值x的随机变量的值。我们可以使用cdf()函数计算CDF。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt
c, s = 2.14, 0.446

x = 1.5
cdf_ = powerlognorm.cdf(x, c, s)

print(cdf_)

输出

0.9740141301157031

解释

在此函数中，我们从scipy.stats模块导入powernorm类，用于处理幂对数正态分布。

方法三：可视化幂对数正态分布

让我们可视化幂对数正态分布。

示例

from scipy.stats import powerlognorm
import numpy as np
import matplotlib.pyplot as plt

c, s = 2.14, 0.446

r = powerlognorm.rvs(c,s, size=1000)

plt.hist(r, bins=30, density=True, alpha=0.5)
plt.title('Power Log-Normal Distribution')
plt.xlabel('Values')
plt.ylabel('Probab')
plt.show()

输出

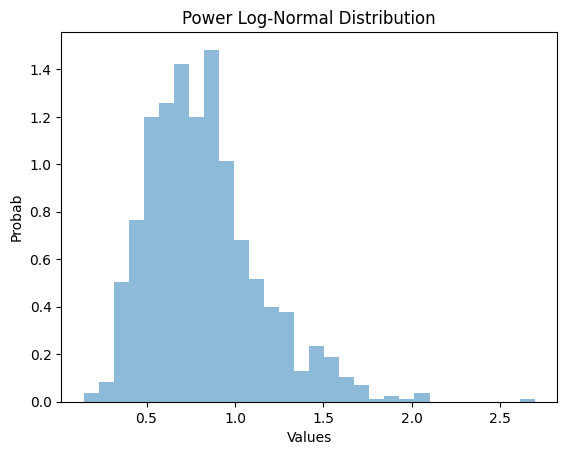
解释

我们导入了用于处理幂对数正态分布和绘制图形的库。像往常一样，我们使用powerlognorm.rvs()方法从幂对数正态分布生成1000个随机值。使用直方图中的hist()函数绘制图形。

因此，在这篇文章中，我们了解了幂对数正态分布。我们看到了使用PDF的各种方法，包括生成随机变量、计算PDF、CDF以及使用直方图可视化分布。此外，我们还看到了如何将我们的数据拟合到（概率密度函数）PDF中。