使用 Python 在统计学中展示幂函数分布

---

在本文中，我们将学习统计学中的幂函数分布。我们将检查可以使用各种方法来分析幂函数分布。在这篇文章中，我们还将了解如何在需要时拟合幂函数分布。在此之前，让我们先了解什么是幂函数分布。

幂函数分布

这是一种用于对数据建模的连续概率分布。使用幂函数，我们可以分析产生某些影响的小事件。使用幂函数，我们可以获取有关罕见事件的详细信息，识别异常值，并可以对极值进行预测。

方法 1：使用 NumPy

在这种方法中，我们将使用 NumPy 库中的 random.number.power 函数从幂函数分布生成随机数。我们还可以根据需要将形状和大小参数传递给函数。

示例

import numpy as np

alpha = 2.0

random_numbers = np.random.power(alpha, size=50)
print(random_numbers)

输出

[0.66577177 0.1679034  0.95589386 0.52785199 0.74796992 0.98980016
 0.56024262 0.93486863 0.74621463 0.34786775 0.68608517 0.75162506
 0.99800817 0.77750768 0.2619546  0.71702682 0.98451869 0.9473717
 0.6938956  0.62181687 0.87593638 0.97820392 0.61942659 0.3998725
 0.60715901 0.41922618 0.69290475 0.22384672 0.94772692 0.42051637
 0.37011727 0.46666447 0.80132086 0.51449008 0.70068973 0.48051619
 0.97054498 0.47957822 0.58914979 0.68553321 0.27976004 0.46894656
 0.82430862 0.66817431 0.54340906 0.61010354 0.61893109 0.0923075
 0.08385714 0.94302131]

解释

在上面的函数中，我们定义了形状参数，然后使用幂函数分布生成 50 个随机数。

random_numbers = np.random.power(alpha, size=50)

结果数组将包含所有这些生成的数字。

方法 2：使用 SciPy

在这种方法中，我们将使用 SciPy 库中的 scipy.Stats.Expon 模块。此模块提供了许多用于处理指数函数分布的技术。我们可以使用 rvs 函数生成随机数，并用于计算 pdf 和 cdf。

示例

from scipy.stats import expon

alpha = 2.0
random_numbers = expon.rvs(scale=alpha, size=100)

x = 0.5
pdf_value = expon.pdf(x, scale=alpha)

cdf_value = expon.cdf(x, scale=alpha)
print(cdf_value)

输出

0.22119921692859515

解释

在此程序中，我们从形状参数为 2.0 的指数函数生成 50 个随机数。在生成数字后，我们使用 rvs 函数计算了某个点 x 的 pdf 和 cdf。

方法 3：使用 Searborn

在此方法中，我们将使用 np.random.power，它将从幂函数分布生成随机数。使用 hist 函数，我们将显示生成的随机数的直方图。

示例

import seaborn as sns

random_num = np.random.power(2.0, size=1000)

sns.distplot(random_num, hist=True, kde=True, bins=30)

输出

解释

在此函数中，我们首先使用幂函数分布生成随机数。以下是生成随机数的行。

random_num = np.random.power(2.0, size=1000)

生成随机数后，我们将使用 matplotlib 库中的 distplot 函数绘制直方图以可视化数据。

方法 4. 使用 Matplotlib

这是一个著名的 python 库，用于绘制图形并绘制数据的视觉表示。我们将使用 matplotlib 中的 plot 函数来可视化幂函数分布。

示例

import matplotlib.pyplot as plt

random_num = np.random.power(2.0, size=1000)

plt.hist(random_numbers, bins=30, density=True, alpha=0.5)
plt.xlabel('Values')
plt.ylabel('Probab')
plt.title('Power-fn Distribution')
plt.show()

输出

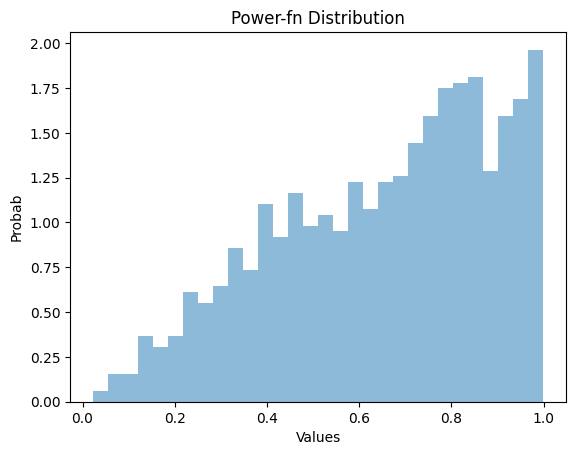
解释

在此方法中，我们使用 np.random.power 从幂函数分布生成随机数。我们使用 matplotlib 库中的 hist 函数来显示生成的随机数的直方图。

方法 5. 将分布拟合到数据

有时在使用 python 时，您会遇到想要拟合幂函数分布的情况。因此，为了执行拟合，我们使用 scipy.stats.exponpow 模块中的 fit 方法，该方法可以根据数据估计形状参数。

示例

from scipy.stats import exponpow
import numpy as np

data = np.array([0.5, 0.6, 0.7, 0.8, 0.9])

params = exponpow.fit(data)

random_num = exponpow.rvs(*params, size=50)
print(random_num)

输出

[0.50115245 0.60597359 0.94355261 1.11336666 0.55644219 1.14871851
 0.83830517 0.84752829 0.52997894 0.79574141 0.59136949 0.67407663
 0.70188119 0.64854262 0.62878517 0.75472879 0.60225659 0.67842203
 0.96134614 0.72039852 0.56041962 0.50058046 0.84463519 0.74643548
 0.60791998 0.52271536 0.79289889 0.65340353 0.92378584 0.51754508
 0.51642979 0.71560587 0.69216641 0.59897395 0.80894948 0.50057274
 0.77434037 0.51578354 0.63737268 0.55335583 0.82872006 0.66339485
 0.50978196 0.68614946 0.73608196 0.58178696 0.85285616 1.03381135
 0.76055906 1.18414065]

因此，我们了解了展示幂函数分布的各种方法。

我们学习了如何从幂函数生成随机数，以及如何计算 PDF（概率密度函数）和 CDF（累积分布函数）。使用 Seaborn 和 Matplotlib，我们绘制了任何统计数据的视觉表示。