使用 Python 展示统计学中的 Tukey-Lambda 分布

---

介绍

统计学家巧妙地将概率分布与相关数据源结合起来，从而为数据库中变量复杂性的广泛而相关的假设提供（或否定）合理性。在这个领域，Tukey Lambda 分布因其独特的特征而脱颖而出。凭借其多功能性，Tukey 分布可以有效地模拟各种形状、尾部和不对称程度不同的数据集。在我们深入探讨 Python 实现之前，首先了解 Tukey-Lambda 分布的基本特征至关重要。

理解 Tukey-Lambda 分布

在 20 世纪 60 年代，John W. Tukey 开发了 Tukey-Lambda 分布——一种统计常数概率分布。该分布足够灵活，可以适应多种形状变化。与通常采用对称和标准化尾部模式的传统分布相比，Tukey-Lambda 分布允许可变性，因为它允许不对称性和可适应的尾部趋势，从而比其前身更全面地适应实际数据集的不规则性。

参数在定义分布中起着核心作用

• Lambda (λ) − 提供非凡的形状控制功能，此特征定义了其他分布在特定限制内分布的区域。方便地从 -∞ 到 +∞ 的变化允许分布中的奇异性与对称性或无序性保持一致。

• 位置 (loc) − 移动此参数会影响数据沿 x 轴的横向分散方式。

• 尺度 (scale) − 控制分布的宽度，分布的尺度因子就像一个主要的操纵者。

使用 Tukey-lambda 分布意味着在没有限制的情况下探索复杂的领域，这得益于其广泛的适用性。

在 Python 中实现 Tukey-Lambda 分布

由于 'numpy'、'matplotlib' 和 'scipy' 的存在，在 python 中操作 Tukey-Lambda 分布简化了流程。通过此过程，我们生成 Tukey-Lambda 分布数据，然后使用编程工具以图形方式描绘其概率密度函数 (PDF)。

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import tukeylambda

# Parameters for the Tukey-Lambda distribution
lam = 0.5  # Lambda parameter
loc = 0    # Location parameter
scale = 2  # Scale parameter

# Generate random data from the Tukey-Lambda distribution
data = tukeylambda.rvs(lam, loc, scale, size=1000)

# Create a histogram of the generated data
plt.hist(data, bins=50, density=True, alpha=0.6, color='g', label='Histogram')

# Plot the PDF of the Tukey-Lambda distribution
x = np.linspace(tukeylambda.ppf(0.01, lam, loc, scale),
   tukeylambda.ppf(0.99, lam, loc, scale), 100)
plt.plot(x, tukeylambda.pdf(x, lam, loc, scale),
   'r-', lw=2, label='PDF')

plt.title('Tukey-Lambda Distribution')
plt.xlabel('Value')
plt.ylabel('Probability Density')
plt.legend()
plt.show()

输出

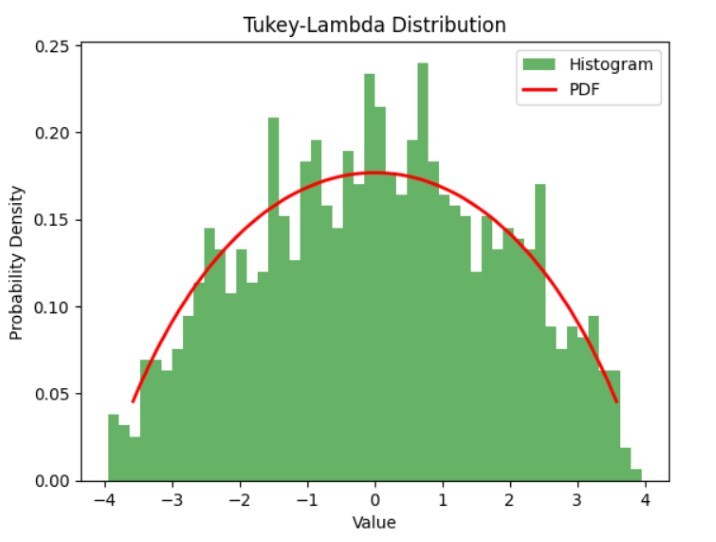
首先，让我们导入项目所需的内容。然后我们定义 Tukey-Lambda 分布的参数：lambda、位置和尺度。使用 'tukeylambda.rvs()'，我们创建了一个包含 100 个数据点的样本集，这些数据点符合预定的规范。

开始生成直方图，我们的重点围绕 'plt.hist()' 指令。经验观察转化为这个描绘数据分布的直方图。执行 'tukey lambda.pdf()' 后，创建与现有图形的叠加图，以进一步阐明变量之间的潜在关系。

从 Tukey-Lambda 分布生成随机样本

示例

import numpy as np
from scipy.stats import tukeylambda

# Define the parameters for the Tukey-Lambda distribution
lam = 1 # Lambda parameter
loc = 0    # Location parameter
scale = 3  # Scale parameter

# Create a Tukey-Lambda random variable
tukey_rv = tukeylambda(lam, loc, scale)

# Generate random samples from the Tukey-Lambda distribution
samples = tukey_rv.rvs(size=10)

# Print the generated samples
print("Generated samples:", samples)

输出

Generated samples: [ 0.72782561 -2.85547765 -2.05191223 -1.49425406 -2.68583332 2.67587261 2.65954901 2.26647354 -2.17126878 2.43279198]

在此代码中，我们首先导入所需的库：numpy 和 scipy.stats.tukeylambda。后者专门用于处理 Tukey-Lambda 分布。然后，我们定义 Tukey-Lambda 分布的参数：Lambda (λ)、位置 (loc) 和尺度构成这些基本值。分布的关键方面与列出的变量相关联。

创建 Tukey-lambda 随机变量需要使用适当选择的参数调用 tukeylambda() 函数。使用 Tukey-Lambda 分布的已定义参数，此随机变量会随机出现。通过使用默认的 Tukey lambda 方法，会从该分布中随机生成样本。此处介绍的练习决定了 10 个实例的选择。

分析具有不同参数的 Tukey-Lambda 分布

示例

from scipy.stats import tukeylambda

def analyze_tukey_distributions(*parameters):
   for params in parameters:
      lam, loc, scale = params
      distribution = tukeylambda(lam, loc, scale)
       
      # Perform analysis on the distribution
      mean = distribution.mean()
      variance = distribution.var()
      
      print(f"For parameters {params}:")
      print(f"Mean: {mean}, Variance: {variance}")
      print()

# Various sets of parameters for Tukey-Lambda distribution
parameters_set1 = (0.5, 0, 2)
parameters_set2 = (-0.2, 1, 1.5)
parameters_set3 = (0.8, -1, 3)

analyze_tukey_distributions(parameters_set1, parameters_set2, parameters_set3)

输出

For parameters (0.5, 0, 2):
Mean: 0.0, Variance: 3.4336293856408293

For parameters (-0.2, 1, 1.5):
Mean: 1.0, Variance: 16.841523810796254

For parameters (0.8, -1, 3):
Mean: -1.0, Variance: 4.253520146569082

解读可视化结果

通过直方图绘制生成的數據的分布，揭示了与 Tukey-Lambda 分布的 PDF 的比較。借助此叠加图，我们可以评估生成的數據与预测分布的符合程度。PDF 偏差表明生成的數據存在与分布的定义特征相矛盾的变化。

应用和意义

Tukey-Lambda 分布的应用多种多样，影响深远。例如，在金融领域，股票回报经常表现出不稳定性，而 Tukey-Lambda 分布可以更好地表示这些非常规模式。在数据看起来失真或尾部长度测量值异常的情况下，生物学可以更多地了解潜在的过程。

最佳实践和注意事项

使用 varargs 和 Tukey-Lambda 分布时，正确记录参数顺序及其意义至关重要。准确的文档将方便用户理解，使他们能够轻松提供正确的参数集。确保函数能够正确处理各种参数组合排列。

结论

Tukey-Lambda 分布是统计学中的一种多用途工具，它可以适应不符合规范的数据，使其有别于传统的分布。使用 Python，研究人员和分析师可以开发一个动态框架。结合分布的 PDF 可视化，可以深入了解其应用和适用性。Tukey-Lambda 分布强调了统计方法在应对现实世界数据挑战方面的灵活性和有效性。