使用 Python 在统计学中展示非中心 F 分布

---

在给定的问题中，我们必须借助 Python 及其库来展示非中心 F 分布。因此，我们将探讨什么是非中心 F 分布以及如何使用 Python 来展示它。

了解非中心 F 分布

非中心 F 分布是统计学中的一种概率分布，它主要用于分析给定数据中的方差。它通过使用非中心参数来使用中心 F 分布，这些非中心参数用于进行偏差。

非中心 F 分布用于确定观察特定统计量的概率。此分布的图形是使用分子和分母的自由度生成的。它还使用非中心参数来显示分布。因此，分布将根据这些参数的值发生变化。

该分布如下所示：

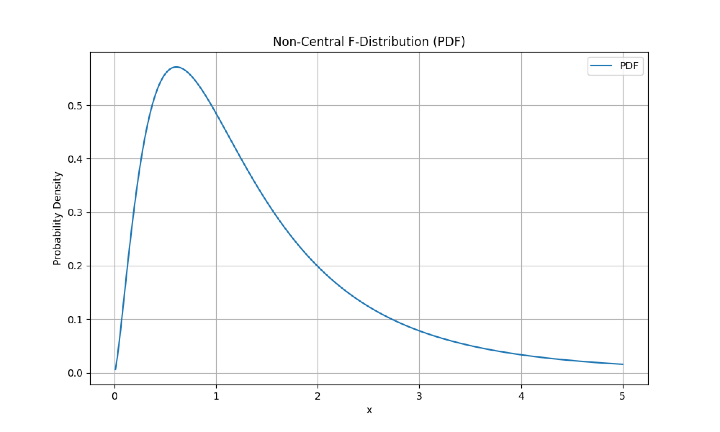
上述问题的逻辑

为了绘制此分布，我们将使用 Python 库“scipy.stats”，在程序中使用它之前，需要将其安装在系统中。为了生成概率密度函数 (PDF) 和累积密度函数 (CDF)，我们将使用 stats.ncf() 函数。为了显示分布，我们必须生成遵循此分布的随机数。因此，我们将通过使用 scipy.stats 库中的 noncentral_f() 函数来获得它。此函数将接受自由度和非中心参数作为输入。通过绘制 PDF 和 CDF，我们可以显示非中心 F 分布。

算法

• 步骤 1 - 首先，我们必须导入 Python 的必要库来显示非中心 F 分布。在我们的程序中，我们将使用 Numpy、Matplotlib 和 Scipy.stats 库。如果这些库未安装在系统上，则需要首先使用 pip install 'library_name' 进行安装，然后我们才能在程序中使用这些库。

import numpy as nmp
import scipy.stats as stats
import matplotlib.pyplot as mt_plt

• 步骤 2 - 导入所需的库后，我们将定义非中心 F 分布的参数，例如分子自由度作为 num_df，分母自由度作为 deno_df，以及非中心参数作为 nc。

# Initialize the required parameters
num_df = 5  # numerator df
deno_df = 10  # denominator df
nc = 1  

• 步骤 3 - 现在，我们将生成用于绘制 F 分布的 x 坐标值。

# initialize the random numbers for x-values
x = nmp.linspace(0.1, 10, 1000)

• 步骤 4 - 接下来，我们将使用 stats.ncf() 函数计算概率密度函数的值并将其命名为 y_pdf，以及累积密度函数的值并将其命名为 y_cdf。

# compute PDF and CDF
y_pdf = stats.ncf.pdf(x, num_df, deno_df, nc)  
y_cdf = stats.ncf.cdf(x, num_df, deno_df, nc)  

• 步骤 5 - 计算所有所需的值后，我们将需要使用 matplotlib 绘制概率密度函数。在我们的绘图中，我们将显示 x 轴标签、y 轴标签和绘图标题。

# plotting the Probability density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_pdf, label='PDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Probability Density')
mt_plt.title('Non-Central F-Distribution (PDF)')
mt_plt.legend()
mt_plt.grid(True)

• 步骤 6 - 现在，我们还将使用 matplotlib 库绘制累积密度函数 (CDF)。

# plotting the cumulative density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_cdf, label='CDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Cumulative Probability')
mt_plt.title('Non-Central F-Distribution (CDF)')
mt_plt.legend()
mt_plt.grid(True)

• 步骤 7 - 在程序的最后，我们将使用 show() 函数显示绘图。

# Show the plots
mt_plt.show()

示例

import numpy as nmp
import scipy.stats as stats
import matplotlib.pyplot as mt_plt

# Initialize the required parameters
num_df = 5  # numerator df
deno_df = 10  # denominator df
nc = 1  

# initialize the random numbers for x-values
x = nmp.linspace(0.1, 10, 1000)

# compute PDF and CDF
y_pdf = stats.ncf.pdf(x, num_df, deno_df, nc)  
y_cdf = stats.ncf.cdf(x, num_df, deno_df, nc)  

# plotting the Probability density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_pdf, label='PDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Probability Density')
mt_plt.title('Non-Central F-Distribution (PDF)')
mt_plt.legend()
mt_plt.grid(True)

# plotting the cumulative density function
mt_plt.figure(figsize=(8, 6))
mt_plt.plot(x, y_cdf, label='CDF')
mt_plt.xlabel('x')
mt_plt.ylabel('Cumulative Probability')
mt_plt.title('Non-Central F-Distribution (CDF)')
mt_plt.legend()
mt_plt.grid(True)

# Show the plots
mt_plt.show()

输出

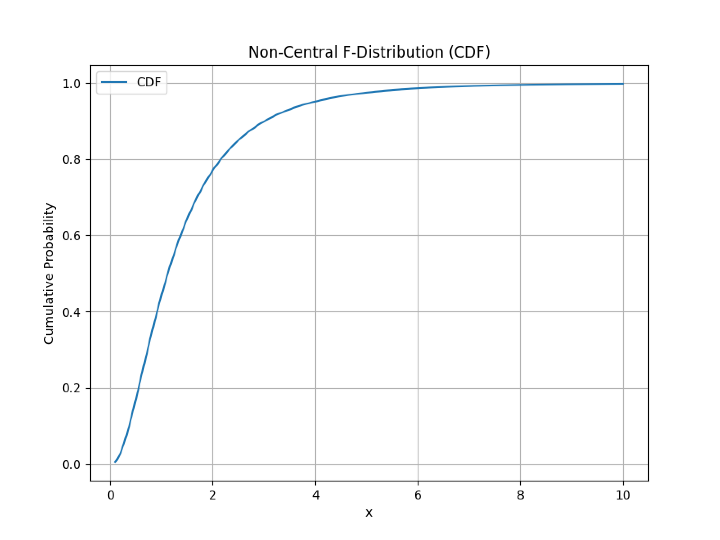
复杂度

生成随机 x 值和绘制非中心 F 分布的复杂度是线性的，为 O(n)，其中 n 是 x 轴上的点数。在我们的代码中，我们生成了 1000 个点来绘制 PDF 和 CDF。这两个密度函数具有相同的复杂度。

结论

在本文中，我们借助 Python 库演示了非中心 F 分布。正如我们使用分子自由度、分母自由度和非中心参数来生成 x 值一样，这导致了线性的复杂度，这对于生成此分布是有效的。