使用 Python 展示统计学中的 Pearson III 型分布

---

Pearson III 型分布是一种在统计学中广泛使用的连续概率分布。它具有偏斜分布。三个参数决定了分布的形状：位置、尺度和形状。发现这种类型的分布将使统计学家能够更有效地分析数据并做出更精确的预测。

我们可以使用 `pearson3.rvs` 函数从分布中生成随机数，并借助 `pearson3.pdf` 函数计算给定点的概率密度函数 (pdf)。

Pearson III 型分布的参数

• 形状参数 - 此参数通过分布的概率密度确定分布的扩展程度。最大值应为 0。当此值小于 0 时，分布是扩展的。

• 位置参数 - 此参数决定分布图的位置。它应该为零。

• 尺度参数 - 此参数决定分布图的尺度。最大值应为 0。当此值小于 0 时，分布是扩展的。

语法

用于从分布中生成随机数。

ran_num = pearson3.rvs(shape, loc, scale, size)

方法 1：这里我们正在计算来自给定分布的随机数

示例 1

从分布中生成 12 个随机数。

from scipy.stats import pearson3

#parameters of the Pearson Type 3 distribution
shape = 2.7
loc = 1.0
scale = 0.7

# Generating random numbers from the distribution
ran_num = pearson3.rvs(shape, loc, scale, size=12)
# Print the numbers
print(ran_num)

输出

[1.78675698 1.2868774  0.79792263 1.73894349 1.06018355 0.90932737
 1.03330347 0.79210384 0.61598714 0.5778327  0.4899408  0.72123621]

在这个例子中，我们首先定义了三个参数（形状、位置、尺度），然后应用 `pearson3.rvs` 函数生成 12 个随机数。

示例 2

从分布中生成并绘制 12 个随机数的直方图。

from scipy.stats import pearson3
import matplotlib.pyplot as plt

#parameters of the Pearson Type 3 distribution
shape = 2.7
loc = 1.0
scale = 0.7

# Generating random numbers from the distribution
ran_num = pearson3.rvs(shape, loc, scale, size=12)

# histogram of the generated random numbers
plt.hist(ran_num, bins=15)  #bins define the number of bars 
plt.xlabel('Random Numbers')
plt.ylabel('Frequency')
plt.title('Histogram of Random Numbers')
plt.show()

输出

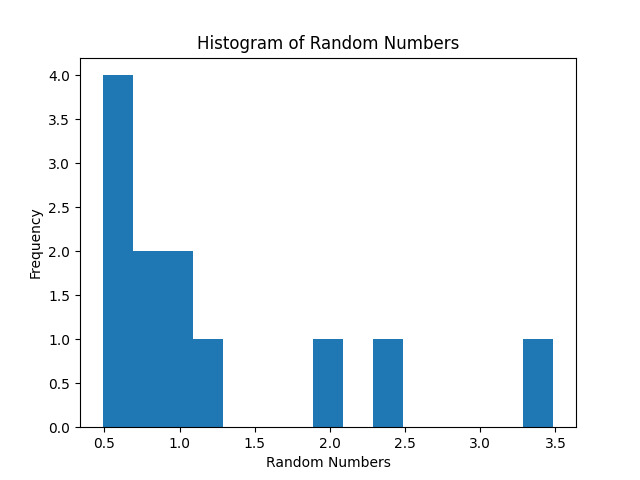
在这个例子中，我们首先定义了三个参数（形状、位置、尺度），然后应用 `pearson3.rvs` 函数生成 12 个随机数。最后，我们绘制了直方图来测量这些随机数。

示例 3

计算从分布中生成的 12 个随机数的均值和中位数。

from scipy.stats import pearson3
import numpy as np

#parameters of the Pearson Type 3 distribution
shape = 2.7
loc = 1.0
scale = 0.7

# Generating random numbers from the distribution
ran_num = pearson3.rvs(shape, loc, scale, size=12)

# Calculating the mean and median of the generated random numbers
mean = np.mean(ran_num)
median = np.median(ran_num)

print("Mean:", mean)
print("Median:", median)

输出

Mean: 0.7719624059755859
Median: 0.6772205996213376

在这个例子中，我们首先定义了三个参数（形状、位置、尺度），然后应用 `pearson3.rvs` 函数生成 12 个随机数，之后我们计算这 12 个随机数的均值和中位数。

方法 2：这里我们正在计算来自给定分布的概率密度函数

语法

用于计算来自分布的概率密度函数。

pdf = pearson3.pdf(value, shape, loc, scale)

示例 1

计算特定点上分布的概率密度函数 (pdf)。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import pearson3

# parameters of the Pearson Type III distribution
shape = 2.7
loc = 1.0
scale = 0.7

# Calculate the PDF of the distribution on specific point
value = 3.5
pdf = pearson3.pdf(value, shape, loc, scale)

print(pdf)

输出

0.015858643122817345

在这个例子中，我们定义了三个参数并给定一个特定值。然后应用 `pearson3.pdf` 函数计算概率密度函数。

示例 2

计算范围为 0 到 10 的分布的概率密度函数 (pdf)。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import pearson3

# parameters of the Pearson Type III distribution
shape = 2.7
loc = 1.0
scale = 0.7


# range of values
value = np.linspace(0, 10, 50)

# Calculate the PDF of the distribution
pdf = pearson3.pdf(value, shape, loc, scale)

print(pdf)

输出

[0.00000000e+00 0.00000000e+00 0.00000000e+00 1.38886232e+00
 7.32109657e-01 4.75891782e-01 3.31724610e-01 2.39563951e-01
 1.76760034e-01 1.32313927e-01 1.00074326e-01 7.62827095e-02
 5.85022291e-02 4.50857115e-02 3.48854378e-02 2.70832764e-02
 2.10857325e-02 1.64563072e-02 1.28704163e-02 1.00845296e-02
 7.91457807e-03 6.22057784e-03 4.89551703e-03 3.85722655e-03
 3.04237200e-03 2.40197479e-03 1.89804851e-03 1.50105698e-03
 1.18798272e-03 9.40852230e-04 7.45605438e-04 5.91225860e-04
 4.69069138e-04 3.72343273e-04 2.95705253e-04 2.34947290e-04
 1.86752271e-04 1.48502788e-04 1.18131774e-04 9.40054875e-05
 7.48317202e-05 5.95877020e-05 4.74634014e-05 3.78168933e-05
 3.01391876e-05 2.40264885e-05 1.91582965e-05 1.52801078e-05
 1.21897366e-05 9.72649439e-06]

在这个例子中，我们定义了三个参数并给定范围为 0 到 10 的值。然后应用 `pearson3.pdf` 函数计算概率密度函数并打印结果。

示例 3

分布的概率密度函数 (pdf) 的可视化表示。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import pearson3

# parameters of the Pearson Type III distribution
shape = 2.7
loc = 1.0
scale = 0.7

# range of values
value = np.linspace(0, 10, 50)

# Calculate the PDF of the distribution
pdf = pearson3.pdf(value, shape, loc, scale)

# Plotting the PDF
plt.plot(value, pdf)
plt.xlabel('value')
plt.ylabel('PDF')
plt.title('Probability Density Function (PDF)')
plt.show()

输出

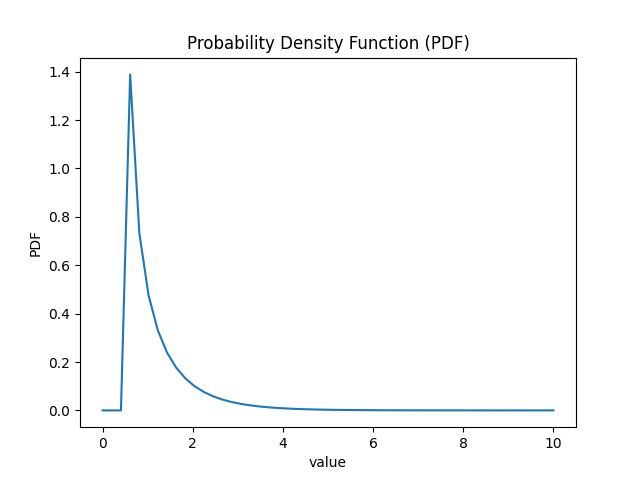
在这个例子中，我们可以看到概率密度函数的图形表示。

结论

总之，Pearson III 型分布是一个重要的概率分布。这种分析在概率论和统计学中占有重要地位。我们可以使用各种库和包，例如 SciPy、NumPy 和 Pandas，在 Python 中对 Pearson III 型分布进行建模。