梯形面积

---

简介

梯形的面积是指梯形在二维平面中所覆盖的区域。梯形是一个凸四边形，只有一对平行边。梯形是一个二维图形。如果我们把它画在纸上，它看起来像一张桌子。在欧几里得几何学的术语中，四边形可以描述为恰好具有四条边和四个顶点的多边形。梯形的边数、角数始终为四，且恒定不变。

现实世界中有很多梯形的例子。梯形的根本用途是梯形法则，它将曲线下的区域分成多个梯形，并计算每个梯形的面积。

梯形

平行四边形也可以被称为有两条平行边的梯形。

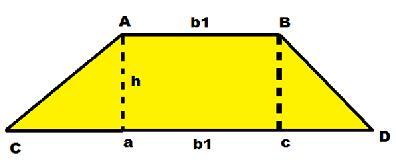
从上图可以看出，AB边和CD边互相平行，而AC边和BD边是非平行边。“h”表示两条平行线之间的距离，代表梯形的高度。

梯形是一个封闭图形或多边形，其边数、顶点数和角数都恰好为四。梯形中的一对平行边也是其对边。

在我们周围有很多梯形的实际例子。

例如，带有梯形表面的桌子。

梯形类型

梯形分为三种类型。这三种类型如下所示。

• 等腰梯形

• 不等边梯形

• 直角梯形

不等边梯形

所有边长不相等梯形称为不等边梯形。

直角梯形

直角梯形至少有两条相邻的直角。一个直角梯形至少有一个直角。

不规则梯形

通常，当我们看到一个四边形，其中一对边平行，而另一对边不相等但相等时，就可以识别出梯形。这些类型的梯形称为规则梯形。对于不规则梯形，非平行边不相等。这就是它们被称为不规则梯形的原因。

梯形的性质

梯形的一些重要性质是：

• 在梯形中，只有一对平行边，它们也是对边。

• 对角线总是相交。

• 梯形的非等边也非平行。除了等腰梯形外，它们不相等。

• 梯形的中位线等于平行边之和的一半。

梯形的中位线

$\mathrm{中位线 =\frac{(AB+ CD )}{2}}$ 其中AB和CD是平行边或底。

对于等腰梯形，腰或非平行边是全等的。梯形的内角和等于360度，即

$$\mathrm{\angle A +\angle B +\angle C +\angle D = 360°}$$

两个相邻角的和是180°。这意味着两个相邻角互补。

梯形的面积

梯形的面积可以通过取梯形两个底的平均值并乘以高来计算。因此，梯形法的面积由下式给出

$$\mathrm{梯形面积,\: A = \frac{h(a+b)}{2}\: 平方单位.}$$

其中“a”和“b”是底

“h”是高。

设等腰梯形ABCD的平行边长分别为a和b。这相当于a是底边长度，b是与a平行的边长。c是两条非平行边的长度，h是等腰梯形的高度。其中

$$\mathrm{AB = a,\: CD = b,\: BC = AD = c}$$

当h垂直地从CD减去并与AB相交于E点时，就会形成一个直角三角形AED，垂直高度为

$$\mathrm{h = \sqrt{c^2 – (a-b)^2}[根据勾股定理]}$$

如你所知，梯形面积的公式为：

$$\mathrm{面积 =\frac{1}{2} h(a+b)}$$

$$\mathrm{等腰梯形面积 = \frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$$

例题

1)如果梯形的三个边长分别为3、4、5，则梯形的面积是多少？

答：我们知道面积由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$给出。

因此，面积为

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{5^2 – (4-3)^2} (4+3)]= \frac{1}{2}\sqrt{24}(7)} \approx 17.08$$

因此，梯形的面积约为17.08。

2)如果梯形的三个边长分别为5、6、7，则梯形的面积是多少？

答：我们知道面积由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$给出。

因此，面积为

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{7^2 – (6-5)^2} (5+6)]= \frac{1}{2} \sqrt{48}(11) } \approx 38.10$$

因此，梯形的面积约为38.10。

3)如果梯形的三个边长分别为7、8、9，则梯形的面积是多少？

答：我们知道面积由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$给出。

因此，面积为

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{9^2 – (8-7)^2} (7+8)]= \frac{1}{2} \sqrt{80}(15) } \approx 67.08$$

因此，梯形的面积约为67.08。

4)如果梯形的三个边长分别为10、11、12，则梯形的面积是多少？

答：我们知道面积由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$给出。

因此，面积为

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{12^2 – (11-10)^2} (11+10)]= \frac{1}{2} \sqrt{143}(21) } \approx 123.86$$

因此，梯形的面积约为123.86。

5)如果梯形的三个边长分别为7、3、2，则梯形的面积是多少？

答：我们知道面积由公式 $\mathrm{\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]}$给出。

因此，面积为

$$\mathrm{=\frac{1}{2} [\sqrt{c^2 – (a-b)^2} (a+b)]= \frac{1}{2} [\sqrt{7^2 – (3-2)^2} (2+3)]= \frac{1}{2} \sqrt{48}(5) } \approx 17.32$$

因此，梯形的面积约为17.32。

结论

平行四边形是具有两对平行边的四边形。但是，梯形是只有一对平行边的四边形。这些平行边显然位于相对位置。最大的平行边通常被认为是梯形的底边。

常见问题

1.梯形有平行边吗？

梯形是只有一对平行边的四边形。这些平行边显然位于相对位置。

2.我们可以说梯形的对角线相等吗？

梯形的对角线不必相等。梯形只有一对平行边。但是，为了使四边形具有相等的对角线，两组线必须平行，例如正方形、矩形等。

3.在梯形中，对角线是否相交于彼此的中点？

梯形的对角线不相交于彼此的中点。如果对角线平分，梯形将变成平行四边形。因此，所有平行四边形都是梯形，但并非所有梯形都是平行四边形。

4.正方形是梯形吗？

是的，矩形必须至少有一对平行边才能成为梯形，另外两条线是否平行并不重要。

5.风筝是梯形吗？

不是，风筝不是梯形，因为它没有一对平行边。