数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
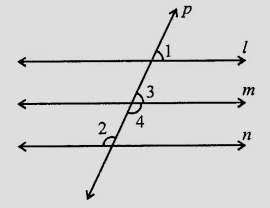
已知：$l \parallel m \parallel n$ 且 $\angle 1 = 60^o$。求解：我们需要求 $\angle 2$。解：从图中可以看出，横截线 $p$ 与直线 $l$、$m$ 和 $n$ 相交。$\angle 1 = 60^o$ $\angle 3 = \angle 1 = 60^o$ (同位角相等) $\angle 3 + \angle 4 = 180^o$ (邻补角) $60^o + \angle 4 = 180^o$ $\angle 4 = 180^o - 60^o$ $\angle 4 = 120^o$ $\angle 2 = \angle 4 = 120^o$ (内错角相等) 因此，$\angle 2 = 120^o$。
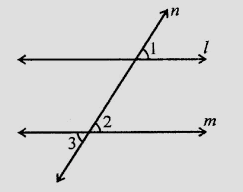
已知：$\angle 1 = 60^o$ 且 $\angle 2 = \frac{2}{3}$ 直角。求解：我们需要证明 $l \parallel m$。解：在给定图中，横截线 $n$ 与两条直线 $l$ 和 $m$ 相交。$\angle 1 = 60^o$ $\angle 2 = \frac{2}{3} \times 90^o = 60^o$ 这意味着，$\angle 1 = \angle 2$。$\angle 1$ 和 $\angle 2$ 是同位角。因此，$l \parallel m$。证毕。
已知：两条直线都垂直于同一条直线。求解：我们需要找出这两条直线之间的关系。解：设 $m \perp l$ 且 $n \perp l$。从图中可以看出，$\angle 1 = 90^o$ 且 $\angle 2 = 90^o$。$\angle 1$ 和 $\angle 2$ 是同位角。这意味着 $m \parallel n$。因此，这两条直线互相平行。
已知：平行四边形的两个不相等的角之比为 $2:3$。求解：我们需要求其所有角度（以度为单位）。解：在平行四边形 ABCD 中，设 $\angle A$ 和 $\angle B$ 是不相等的角。这意味着 $\angle A : \angle B = 2 : 3$。设 $\angle A = 2x$，则 $\angle B = 3x$。$\angle A + \angle B = 180^o$ (内错角互补) $2x + 3x = 180^o$ $5x = 180^o$ $x = \frac{180^o}{5}$ $x = 36^o$ 因此，$\angle A = 2x = 2(36^o) = 72^o$ $\angle B = 3x = 3(36^o) = 108^o$ 对角相等... 阅读更多
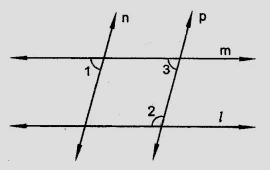
已知：$l \parallel m$，$n \parallel p$ 且 $\angle 1 = 85^o$。求解：我们需要求 $\angle 2$。解：$n \parallel p$，这意味着 $\angle 1 = \angle 3$ (同位角相等) $\angle 3 = \angle 1 = 85^o$ $m \parallel l$，因此 $\angle 3 + \angle 2 = 180^o$ (内错角互补) $85^o + \angle 2 = 180^o$ $\angle 2 = 180^o - 85^o$ $\angle 2 = 95^o$ 因此，$\angle 2 = 95^o$。
丙烯酸纤维的用途如下：用于制作毛衣和运动服，以及靴子和手套的内衬。它也用于制作家具织物和地毯。它还可以用于制作毛皮和许多不同的针织服装。
尼龙或涤纶等合成纤维与天然纤维不同。它们遇热会熔化。如果合成纤维制成的衣服着火，将非常危险。织物会熔化并粘在穿着者身上。因此，我们在厨房工作时不应穿着它。
我们应该在夏天购买棉衬衫，因为棉花可以吸收我们身体的汗水并使其蒸发到空气中。它还可以抑制细菌生长，不会引起任何皮肤过敏。
天然纤维的原料主要来自植物和动物。这需要砍伐大量树木，导致森林砍伐。但合成纤维的原料主要是煤等石化产品。因此，合成纤维的制造有助于保护森林。
塑料是一种像合成纤维一样的聚合物。塑料中单元的排列可以是线性的或交联的。塑料制品具有各种形状和尺寸。它易于成型，可以塑造任何形状。它可以回收、重复使用、染色、熔化，可以轧成薄片或制成线材。五种常用的塑料制品是：玩具、梳子、容器、餐具、电开关。