数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
正确答案：(a) 盐水 解释：盐水是盐溶液。加热时，水会蒸发，留下盐作为残留物。
正确答案：(b) 氢氧化镁乳 解释：氢氧化镁乳是氢氧化镁在水中的悬浮液。它具有牛奶状外观。
正确答案：(b) 黄铜 解释：黄铜是铜和锌的合金。它是固体在固体中溶液的一个例子。
正确答案：(c) 腐蚀，它是化学变化 解释：铁的生锈被称为腐蚀，它导致形成新的化合物。因此，它是一种化学变化。空气和湿气作用于铁会将其转化为氧化物。这个过程被称为生锈。
正确答案：(d) 均相混合物，不显示丁达尔效应 解释：硫完全溶解在二硫化碳中。因此，它是一种均相溶液。由于溶质的颗粒太小而无法散射光，因此它们不会引起丁达尔效应。
已知：三角形的一个角是 75 度。另外两个角的差是 35 度。求解：我们必须找到最大角的度数。解答：设三角形为 ABC，其中∠A=75°，且∠B>∠C。根据三角形的角和性质，∠A+∠B+∠C=180°75°+∠B+∠C=180°∠B+∠C=180°-75°=105°......(i)根据题意，∠B-∠C=35°............(ii)将(i)和(ii)相加，我们得到，∠B+∠C+∠B-∠C=105°+35°2∠B=140°∠B=70°这意味着，70°+∠C=105°∠C=105°-70°=35°最大角的度数是 75°。阅读更多
"\距离=三角形1的面积+矩形2的面积+三角形3的面积+三角形4的面积$=\frac{1}{2}\times2\times10+2\times10+\frac{1}{2}\times1\times10+\frac{1}{2}\times1\times10$$=10+20+5+5$$=40$因此，距离$=40\ m$对于位移：在$\boxed{1}$中，速度变化$\Delta v=v_2-v_1=10-0=10\ m$时间变化$\Delta t=t_2-t_1=2-0=2\ s$因此，位移$d_1=\Delta v\times\Delta t=10\times2=20\ m$在$\boxed{2}$中，速度均匀，因此，速度变化$\Delta v=v_2-v_1=10-10=0$时间变化$\Delta t=t_2-t_1=4-2=2$因此，位移$d_2=\Delta v\times\Delta t=0\times2=0$在$\boxed{3}$中，速度变化$\Delta v=v_2-v_1=0-10=-10\ m/s$时间变化$\Delta t=t_2-t_1=5-4=1\ s$因此，位移$d_3=\Delta v\times \delta t=-10\times1=-10\ m$在$\boxed{4}$中，速度变化$\Delta v=v_2-v_1=-10-0=-10\ m/s$时间变化$\Delta t=t_2-t_1=6-5=1\ s$因此，位移$d_4=\Delta v\times\Delta t$$=-10\times1=-10\ m$图表中的总位移$=d_1+d_2+d_3+d_4$$=20+0-10-10$$=0$因此，根据给定的图表，... 阅读更多
已知：一个顶部开口的桶由金属板制成，呈圆台形。桶的深度为\( 24 \mathrm{~cm} \)，其上下圆形底部的直径分别为\( 30 \mathrm{~cm} \)和\( 10 \mathrm{~cm} \)。求解：我们必须找到制作该桶所用金属板的成本，每\( 100 \mathrm{~cm}^{2} \)的成本为\( ₹ 10 \)。解答：桶的上半径$\mathrm{R}=\frac{30}{2}$$=15 \mathrm{~cm}$桶的下半径$r=\frac{10}{2}$$=5 \mathrm{~cm}$桶的高度$h=24 \mathrm{~cm}$因此，斜高为... 阅读更多
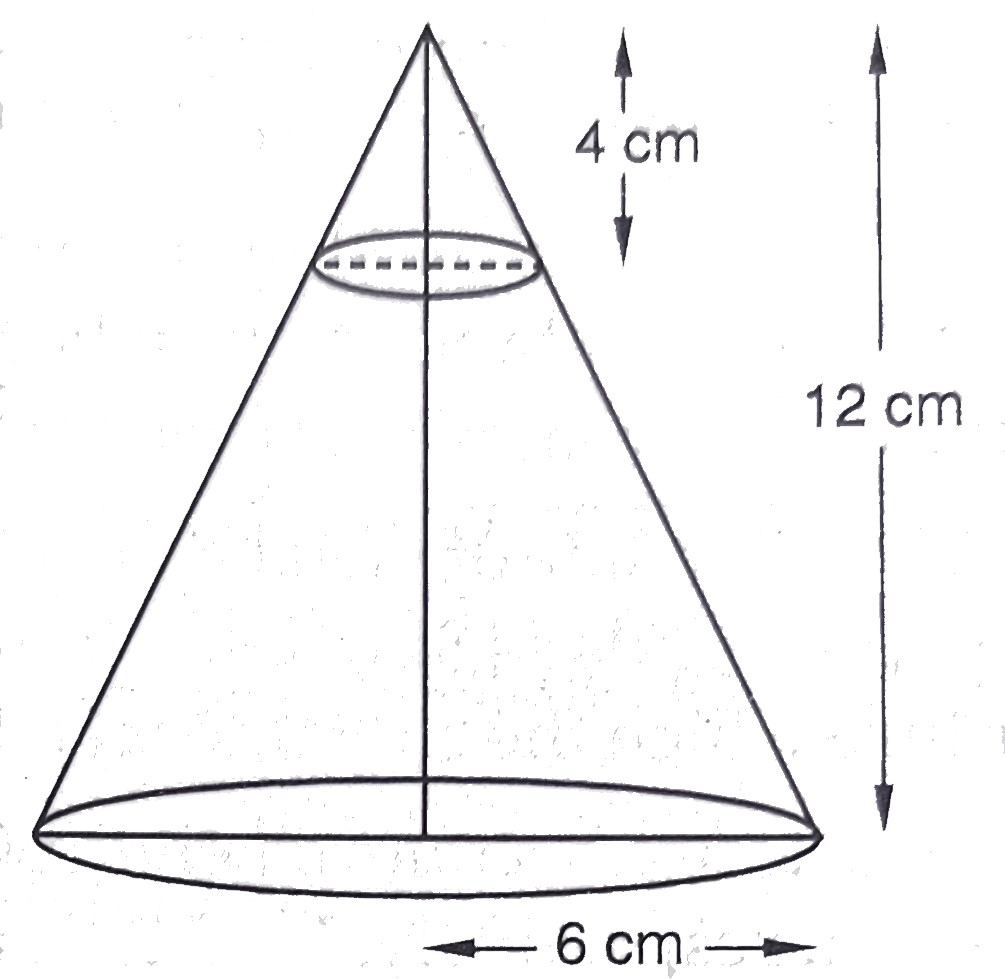
"\已知：如图所示，从高为\( 12 \mathrm{~cm} \)和底半径为\( 6 \mathrm{~cm} \)的实心圆锥顶部，通过平行于底面的平面移除一个高为\( 4 \mathrm{~cm} \)的圆锥。求解：我们必须找到剩余实心体的总表面积。解答：圆锥的总高度$= 12\ cm$圆锥底部的半径$= 6\ cm$形成的圆台的高度$= 12 - 4$$= 8\ cm$设$r$为切出的圆锥的半径。这意味着，$\frac{r}{6}=\frac{4}{12}$$r=\frac{6 \times 4}{12}$$=2 \mathrm{~cm}$设$l$为整个... 阅读更多
已知：一个水桶呈圆台形，容积为\( 12317.6 \mathrm{~cm}^{3} \)水。桶的顶部和底部的圆形底面半径分别为\( 20 \mathrm{~cm} \)和\( 12 \mathrm{~cm} \)。 求解：求水桶的高度和制作水桶所需的金属板面积。解：水桶体积 = 12308.8 cm³水桶上底半径 \(r_1 = 20\ cm\)水桶下底半径 \(r_2 = 12\ cm\)设水桶高度为 h。因此，\(12308.8=\frac{\pi}{3}[r_{1}^{2}+r_{1} r_{2}+r_{2}^{2}] \times h\)
\( \Rightarrow 12308.8=\frac{3.14}{3}[20^{2}+20 \times 12+12^{2}] \times h\)
\( \Rightarrow 12308.8=\frac{3.14}{3}[400+240+144] ... 阅读更多