数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：步枪的质量，m1 = 4 kg子弹的质量，m2 = 50 g = 0.05 kg子弹的初速度，v2 = 35 m/s求：步枪的初始反冲速度，v1。解：设步枪的反冲速度 = v1发射前-子弹、步枪和子弹都处于静止状态，因此，初速度 (v) 将为零。因此，步枪和子弹系统的总初动量为-=(m1+m2)×v (因为 p=m×v，其中 p=动量，m=质量，v=速度)=(m1+m2)×0=0 (因为 v=0)发射后-子弹的动量 = m1v1步枪的动量 ... 阅读更多
标量：它只有大小。例如，长度、面积、速度、质量、密度、压力、温度、功、能量等。矢量：它既有大小又有方向。例如，位移、速度、加速度、力、阻力等。它用箭头表示。箭头的头部表示该量移动的方向，箭头所在数字表示物理量的大小。因此，位移是矢量量，因为它既有大小又有方向。
"\(a) 在呼吸过程中，肺泡为肺部提供表面积，用于在呼吸过程中进行氧气和二氧化碳与血液之间的交换。(b) 水生生物的呼吸频率远快于陆生生物，因为水生动物呼吸溶解在水中的氧气。水中溶解氧的含量比大气中氧气的含量少。因此，水生生物的呼吸频率远快于陆生生物。(c) 在葡萄糖分解途径中：(i) 丙酮酸 - 3 个碳原子组成的分子，... 阅读更多
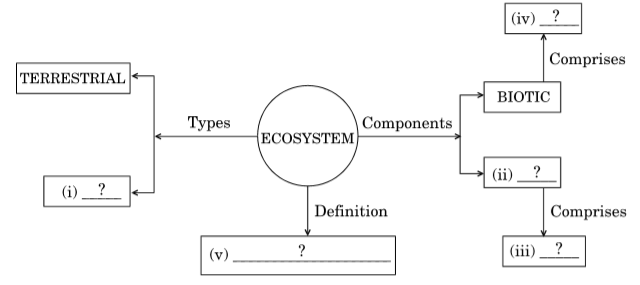
"\答案：(i) 水生生态系统(ii) 非生物(iii) 土壤、水、风(iv) 植物和动物(v) 生态系统可以定义为特定环境中生物和非生物成分之间的相互作用。
正确答案：(C) 绿色解释：如果将 10 mL 的 H2SO4 与 10 mL 浓度相同的 Mg(OH)2 混合，所得溶液的 pH 值将为 7，因为它是一种强酸-强碱滴定。给定的方程式为 $H_2SO_4 + Mg(OH)_2 \rightarrow MgSO_4 + 2 H_2O$。众所周知，pH 值为 7 时，通用指示剂呈绿色，因此，(c) 是正确选项。
正确答案：(B) XY2解释：X 的电子构型为 2,8,2，因此，X 的化合价为 2Y 的电子构型为 2,8,7，因此，Y 的化合价为 1。交叉它们的化合价并将其表示为下标，我们得到化学式为 XY2。
(a) 在正碳电极上，产生氧气。(b) 在负碳电极上，产生氢气。解释在使用碳电极电解酸化水期间，$O\ ^{2-}$ 离子在正碳电极（阳极）上被氧化，因此氧气在阳极释放。而 $H^+$ 离子在负碳电极（阴极）上被还原，因此氢气在阴极释放。
正确答案：(C) 第 17 族和第 3 周期解释：元素氧化物的酸性在周期表中从左到右增强。这意味着周期表中最右侧的元素将具有最酸性的氧化物。
已知：两个有理数：$-\frac{12}{15}$ 和 $65$。要做的：写出任意四个有理数。解：给定两个数字：$-\frac{12}{15}$ 和 $65$。两个有理数 $-\frac{12}{15}$ 和 $65$ 之间的有理数为：$-\frac{11}{15},\ -\frac{10}{15},\ -\frac{9}{15},\ -\frac{8}{15}$。
已知：多项式 $p^{4}-256$。要做的：求多项式的次数。解：给定多项式为：$p^{4}-256$。这里变量 x 的最大幂为 4。因此，给定多项式的次数为 4。