解答:设对角线 AC 和 BD 相交于点 O。由于三角形中任意两条边的长度之和大于第三条边的长度,因此:在△AOB 中,AB < OA + OB ……….(i) 在△BOC 中,BC < OB + OC ……….(ii) 在△COD 中,CD < OC + OD ……….(iii) 在△AOD 中,DA < OD + OA ……….(iv) ⇒ AB + BC + CD + DA < 2OA + 2OB + 2OC + 2OD ⇒ AB + BC + CD + DA < 2[(AO + OC) + (DO + OB)] ⇒ AB + BC + CD + DA < 2(AC + BD) 因此,得证。
已知:$\frac{689}{477}$ 解题步骤:我们需要将分数 $\frac{689}{477}$ 约简到最简形式。 解答:$\frac{689}{477}$ = $\frac{13 \times 53}{3 \times 3 \times 53}$ = $\frac{13}{3 \times 3}$ = $\mathbf{\frac{13}{9}}$ 所以,$\frac{689}{477}$ 的最简形式是 $\frac{13}{9}$。
罗马数字系统:罗马数字系统在中世纪后期广泛应用于欧洲。符号为 I、V、X、L、C、D 和 M,分别代表 1、5、10、50、100、500 和 1000。罗马数字仍然用于钟表和国王、君主、教皇的名字,例如查理四世、教皇保罗二世、理查三世等等。 罗马数字系统中没有零。 印度-阿拉伯数字系统:目前,印度-阿拉伯数字系统在世界各地使用。该系统大约在公元 7 世纪在印度发展起来。最初,它有…… 阅读更多
已知:$? \div \frac{8}{5} = \frac{3}{5}$ 解题步骤:找出缺失的数字 解答:设缺失的数字为 $y$ $y \times \frac{8}{5} = \frac{3}{5}$ 交叉相乘,所以 $y = \frac{3}{5} \times \frac{5}{8} = \frac{3}{8}$ 所以,缺失的数字的最简分数形式是 $\frac{3}{8}$
已知:64 和 84。要验证:我们需要验证 64 和 84 的最大公约数和最小公倍数之间的关系。解答:最大公约数和最小公倍数之间的关系如下;最大公约数 $\times$ 最小公倍数 = 这两个数的乘积 所以,计算 64 和 84 的最小公倍数和最大公约数。64 和 84 的质因数分解;64 = 2 $\times$ 2 $\times$ 2 $\times$ 2 $\times$ 2 $\times$ 2 = 2⁶ 84 = 2 $\times$ 2 $\times$ 3 $\times$ 7 = 2² $\times$ 3 $\times$ 7 因此,LCM (64,84) = 2⁶ $\times$ 3 $\times$ 7 = 1344 HCF (64,84) = 2² = 4 现在,最大公约数 $\times$ 最小公倍数 = 这两个数的乘积 4 $\times$ 1344 = 64 $\times$ 84 5376 = 5376 所以,验证了 64 和 84 的最大公约数和最小公倍数之间的关系。
已知:$\frac{5}{18} \div \square=\frac{2}{3}$ 解题步骤:找出缺失的数字,并将其表示为最简分数。 解答:设未知数为 (x)。$\frac{5}{18}$ 除以 $x$ = $\frac{2}{3}$ $\frac{5}{18}$ = $\frac{2}{3} \times x$ $\frac{5}{18}$ = $\frac{2x}{3}$ $\frac{2x}{3}$ = $\frac{5}{18}$ $x$ = $\frac{5}{18}$ $\times$ $\frac{3}{2}$ $x$ = $\frac{5 \times 3}{18 \times 2}$ $x$ = $\frac{5 \times 1}{6 \times 2}$ [$3 \times 6 = 18$] $x$ = $\frac{5}{12}$ 因此,$x= \frac{5}{12}$
已知:$\frac{9}{11} \div \frac{54}{55}$。解题步骤:计算下列算式,并将答案表示为最简分数。解答:$\frac{54}{55}$ 当它变成分子时变成 $\frac{55}{54}$,=$\frac{9}{11} \times \frac{55}{54}$=$\frac{9}{1} \times \frac{5}{54}$ [$11 \times 5 = 55$]=$\frac{1}{1} \times \frac{5}{6}$ [$9 \times 6 = 54$] =$\frac{5}{6}$ 因此,$\frac{9}{11} \div \frac{54}{55}$ 的最简形式是 $\frac{5}{6}$
物理天平(或梁式天平)的工作原理是力矩原理。根据力矩原理,在平衡状态下,逆时针力矩之和 = 顺时针力矩之和。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP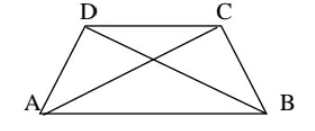 "\
"\