数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
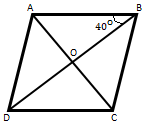
已知：ABCD 是一个菱形，其中角 ABD = 40o。求：这里我们要求出角∠BAC、∠BCD 和∠ADC 的值。解：菱形的对角线互相垂直平分：因此，在∆AOB 中：∠BOA + ∠OAB + ∠ABO = 180o 90o + ∠OAB + 40o = 180o ∠OAB = 180o - (90o + 40o) ∠OAB = 50o i)∠BAC = ∠OAB ∠BAC = 50o ii)∠BDC = ∠ABD (内错角) ∠BDC = 40o iii)∠ACD = ∠BAC (内错角) ∠ACD = 50o
已知：两个有理数的和 = $\frac{-5 }{8}$ 一个数 = $\frac{7}{16}$ 求：求另一个有理数 解：另一个数 = $x$ $x+\frac{7}{16} = \frac-{5}{8}$ $x= -\frac{7}{16} \frac-{5}{8}$ 这里分母不同，所以求 8 和 16 的最小公倍数 8 和 16 的最小公倍数是 16 $x$ = $\frac{-5 \times 2}{8 \times 2} - \frac{7}{16}$ $x = \frac{-10}{16} - \frac{7}{16}$ $x = \frac{-10-7}{16}$ $x = \frac{-17}{16}$ 所以，另一个数是 $\frac{-17}{16}$
已知：两个数的最大公约数 = 4 两个数的最小公倍数 = 168 求：求另一个数 解：第一个数 = 12 另一个数 = $x$ 两个数的积 = 最小公倍数 × 最大公约数 $x \times 12 = 最小公倍数 \times 最大公约数$ $x \times 12 = 168 \times 4$ $x \times 12 = 672$ $x = \frac{672 }{ 12} = 56$ $ x = 56$ 因此，另一个数是 56
已知：筹集的总金额 = 7776 卢比 每张票的价格 = 48$\frac{ 3}{5}$ 卢比 求：这里我们要求出出售的门票数量。解：设出售的门票总数为 = $x$ 一张票的成本 = 48$\frac{3}{5}$ 卢比 = $\frac{243}{5}$ 卢比 $x$ 张票的成本 = $\frac{243x}{5}$ 卢比 因此，$\frac{243x}{5}\ =\ 7776$$x\ =\ 7776\ \times\ \frac{5}{243}$$x\ =$ 160 所以，出售的门票数量是 160。
正确答案：C 最早的工具是鹅卵石工具。
已知：15 个观测值的平均值为 98 求：求所有观测值的总和 解：平均值 = $\frac{所有观测值的总和}{观测值的个数}$ 平均值 = 98 观测值的个数 = 15 98 = $\frac{所有观测值的总和 }{ 15}$ 改写，$\frac{所有观测值的总和}{15} = 98$ 所有观测值的总和 = $98 \times 15$ 因此，所有观测值的总和 = 1470
已知：PQRS 是一个矩形，从 S 到 PR 的垂线 ST 将角 S 分成 2:3 的比例。求：这里我们要求出角 TPQ 的值。解：现在，∠PSR = 90°已知，从 S 到 PR 的垂线 ST 将角 S 分成 2:3 的比例。将 90° 角分成 2:3 的比例。$2x + 3x = 90°$$5x = 90°$$x = 18°$因此，$2x = 2 \times 18 = 36°$ 并且，$3x = 3 \times 18 = 54°$ 所以，∠PST = 36° 现在，在∆PST 中；∠PST + ∠PTS + ∠TPS = ... 阅读更多
以下是蒸发活动步骤。步骤 1. 取一个玻璃杯并装满水。步骤 2. 在阳光明媚的天气里，将一杯水放在家外面。步骤 3. 标记初始水位 您会观察到水位下降了。这意味着水从玻璃表面蒸发了。
已知：4x2 + 9y2 + 16z2 + 12xy − 24yz − 16xz 求：我们必须分解因式 4x2 + 9y2 + 16z2 + 12xy − 24yz − 16xz 解：4x2 + 9y2 + 16z2 + 12xy − 24yz − 16xz = (2x)2 + (3y)2 + (-4z)2 + 2(2x)(3y) + 2(3y)(-4z) + 2(2x)(-4z) 使用 (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac = (2x + 3y - 4z)2 = (2x + 3y - 4z) (2x + 3y - 4z)