数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：$x = -2$ $y = 4$ 解题步骤：a) $5y - 4x$ 将 $x$ 和 $y$ 的值代入 $5y - 4x$ $5(4) - 4(-2) = 20 - (-8) = 20 + 8 = 28$ 所以，答案是 28。b) $\frac{1}{x} - y + 3$ 将 $x$ 和 $y$ 的值代入 $\frac{1}{-2} - 4 + 3 = \frac{-1}{2} - 1 = \frac{-3}{2}$ 所以，答案是 $\frac{-3}{2}$
已知：给定分数为 $\frac{3}{11}$ 解题步骤：我们要写出 $\frac{3}{11}$ 的小数形式 被除数 = 3 除数 = 11 0.2727113.00000 3022 80 77 30 22 80 77 因此，$\frac{3}{11} = 0.2727.....$ $\frac{3}{11}$ 的小数形式是 $0.2727....$
已知：给定的数字是 36 和 300。 解题步骤：我们要绘制给定数字的因数树。 解：36 的因数树： 36 / \ 2 18 / \ 2 9 / \ 3 3 300 的因数树： 300 / \ 2 150 / \ 2 75 / \ 3 25 / \ 5 5
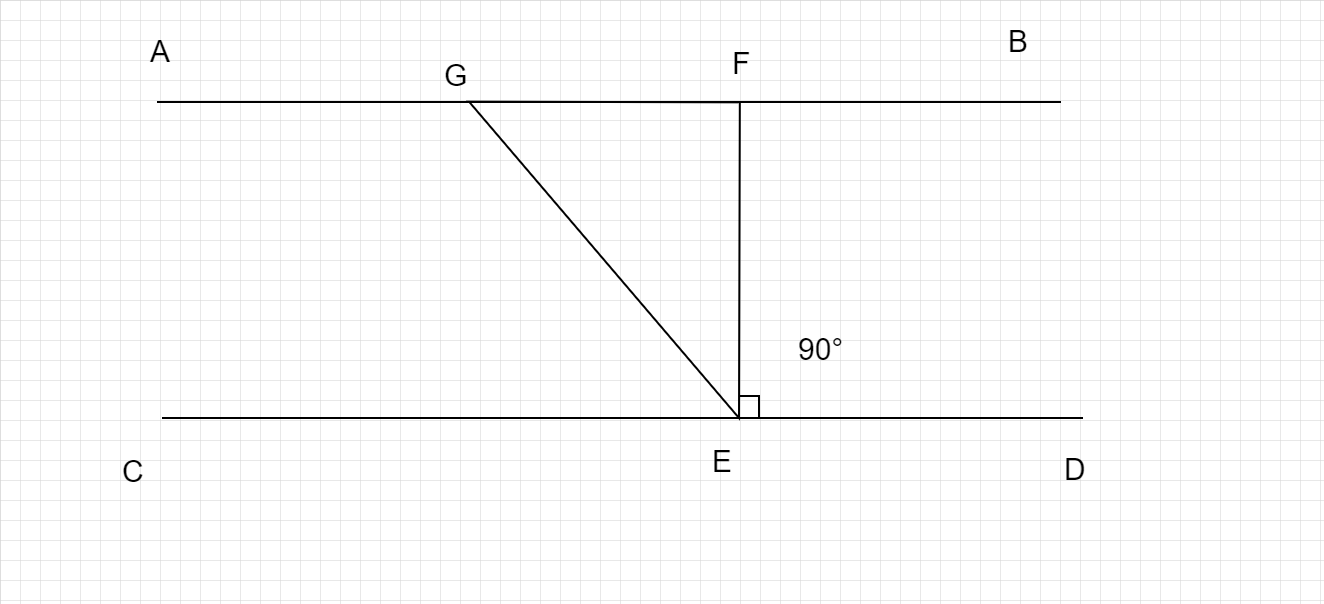
"\已知：$AB \parallel CD$，$EF$ 垂直于 $CD$。$\angle GED = 120^o$。 解题步骤：我们需要找到 $\angle GEC$，$\angle EGF$，$\angle GEF$ 解：$\angle GEF + \angle CEG = 120^o$ $120^o = \angle GEF + 90^o$ $\angle GEF = 120^o - 90^o$ $\angle GEF = 30^o$ $CD$ 是一条直线。因此，$\angle GED + \angle CEG = 180^o$ $120^o + \angle CEG = 180^o$ $\angle CEG = 180^o - 120^o$ $\angle GEC = 60^o$ 在三角形 $GFE$ 中，$\angle GFE + \angle GEF + \angle EGF = 180^o$ $90^o + 30^o + \angle EGF = 180^o$ $\angle EGF = 180^o - 120^o$ $\angle EGF = 60^o$。$\angle GEF = 30^o$，$\angle GEC = 60^o$ $\angle EGF = 60^o$。
已知：给定的数字是 2160。 解题步骤：我们要用因数树方法分解给定的数字。 解：2160 的因数树是， 2160 / \ 2 1080 / \ 2 540 / \ 2 270 / \ 2 135 / \ 3 45 / \ 3 15 / \ 3 5 / \ 5 1 因此，2160 的因数是 $2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 \times 5$
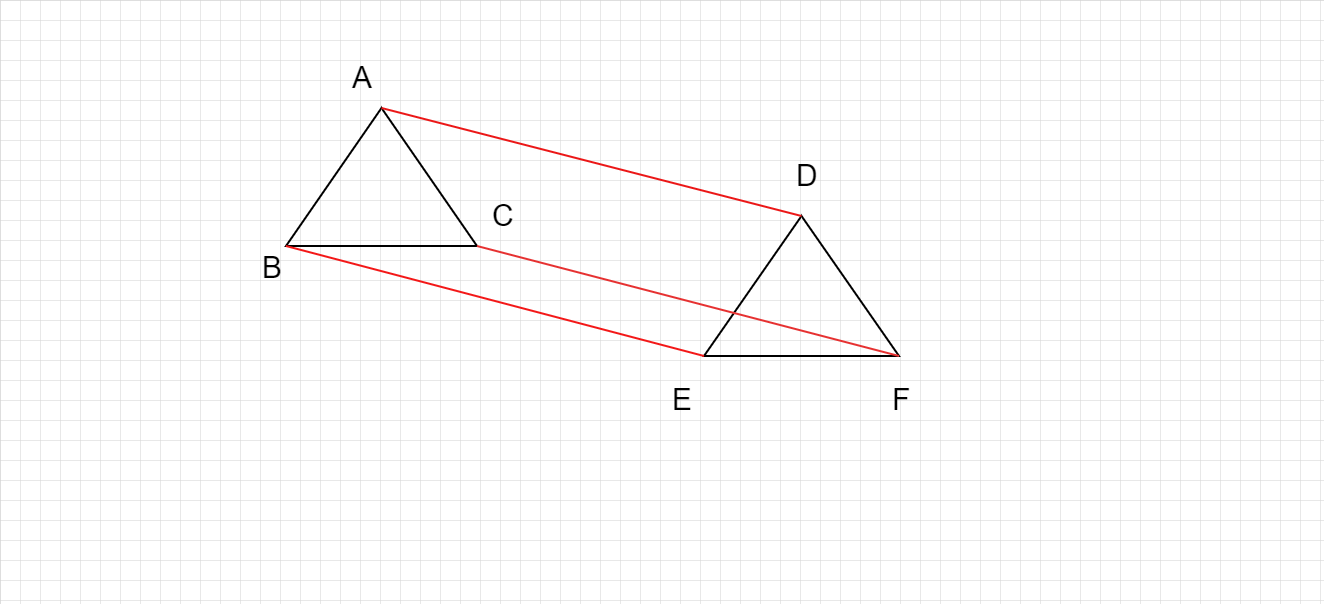
已知：$AB = DE$，$AB \parallel DE$，$BC \parallel EF$。 解题步骤：我们需要证明 (i) 四边形 ABED 是平行四边形 (ii) 四边形 BEFC 是平行四边形 (iii) $AD \parallel CF$ 且 $AD = CF$ (iv) 四边形 ACFD 是平行四边形 (v) $AC = DF$ (vi) $\Delta ABC \cong \Delta DEF$ 解：(i) $AB = DE$。如果一对对边相等且平行，则四边形是平行四边形。因此，ABED 是平行四边形。(ii) $BC = EF$ 且 $BC \parallel EF$。如果一对… 阅读更多