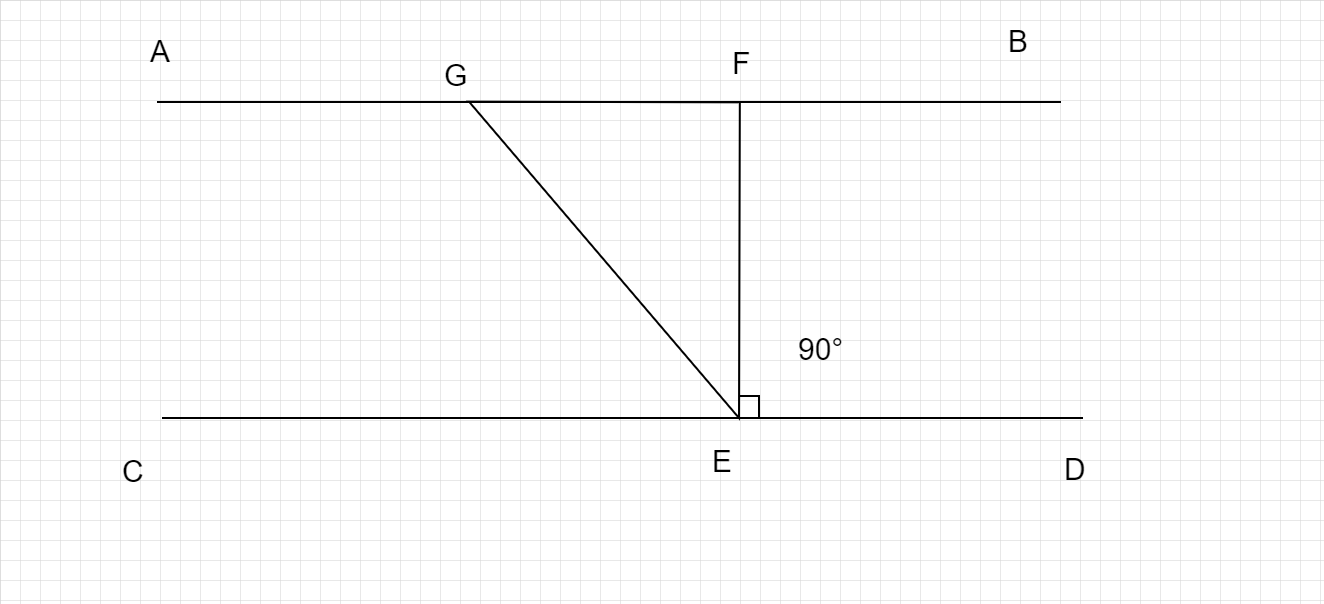
如图，$\displaystyle AB\ \parallel \ CD$，且$EF \perp CD$，$\angle GED = 120°$。求 $\angle GEC , \angle EGF , \angle GEF$
"\n

已知

$AB \parallel CD$ 且 $EF$ 垂直于 $CD$。

$\angle GED = 120^o$。

求解

我们需要求出 $\angle GEC, \angle EGF, \angle GEF$

解答

$\angle GEF + \ angle CEG = 120^o$

$120^o = \angle GEF + 90^o$

$\angle GEF = 120^o-90^o$

$\angle GEF = 30^o$

$CD$ 是一条直线。

因此，

$\angle GED + \angle CEG = 180^o$

$120^o+\angle CEG = 180^o$

$\angle CEG = 180^o-120^o$

$\angle GEC = 60^o$

在三角形 $GFE$ 中，

$\angle GFE + \angle GEF+ \angle EGF= 180^o$

$90^o+30^o+\angle EGF= 180^o$

$\angle EGF= 180^o-120^o$

$\angle EGF= 60^o$。

$\angle GEF = 30^o$ , $\angle GEC = 60^o$

$\angle EGF= 60^o$。

教程点

更新于: 2022年10月10日

40 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习