如图3所示，∠ACB = 90°，且CD ⊥ AB，证明CD² = BD × AD。

已知：∠ACB = 90°，且CD ⊥ AB

求证：CD² = BD × AD

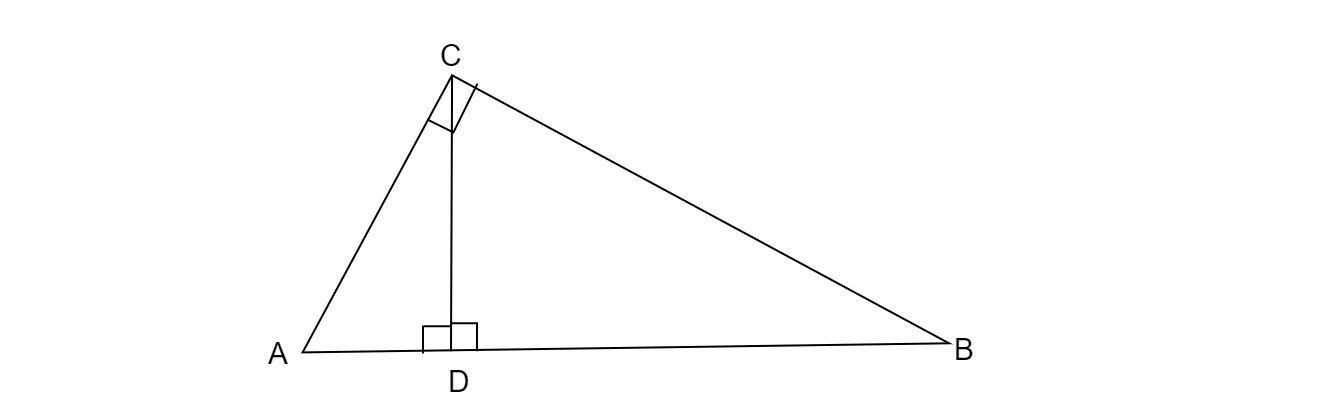
已知CD ⊥ AB。

∠ACB = 90°

在△ACD中，根据勾股定理

(AC)² = (AD)² + (CD)² ..............(i)

在△CDB中，根据勾股定理

(CB)² = (BD)² + (CD)² ..............(ii)

同理，在△ABC中

(AB)² = (AC)² + (BC)² ..............(iii)

因为AB = AD + BD ..............(iv)

将方程(iv)两边平方，

得到

(AB)² = (AD + BD)²

所以，AB² = AD² + BD² + 2 × BD × AD

由方程(iii)得到

AC² + BC² = AD² + BD² + 2 × BD × AD

将方程(i)中AC的值和方程(ii)中BC的值代入，得到

(AD)² + (CD)² + (BD)² + (CD)² = AD² + BD² + 2 × BD × AD

⇒ 2CD² = 2 × BD × AD

⇒ CD² = BD × AD

因此，证明了CD² = BD × AD。