两条直线$AB$和$CD$相交于点$O$，使得$BC$等于且平行于$AD$。证明直线$AB$和$CD$互相平分。
已知
两条直线$AB$和$CD$相交于点$O$，使得$BC$等于且平行于$AD$。
要求
我们必须证明直线$AB$和$CD$互相平分。
解答
$BC = AD$ 且 $BC \parallel AD$
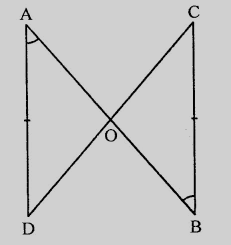
在$\triangle AOD$和$\triangle BOC$中，
$AD = BC$
$\angle A = \angle B$ (内错角相等)
$\angle D = \angle C$ (内错角)
因此，根据ASA公理，
$\triangle AOD \cong \triangle BOC$
这意味着，
$AO = OB$ (全等三角形对应边相等)
$AO = OC$ (全等三角形对应边相等)
因此，$AB$和$CD$互相平分于点$O$。
- 相关文章
- 以点$O$为圆心画一个圆。画出它的两条弦$AB$和$CD$，使得$AB$不平行于$CD$。画出$AB$和$CD$的垂直平分线。它们在何处相交？
- 在图中，射线$AB$和$CD$相交于$O$。当$x = 60^o$时，确定$y$。
- 在图中，射线$AB$和$CD$相交于$O$。当$y = 40^o$时，确定$x$。
- 在图3中，$\angle ACB = 90^{o}$且$CD \perp AB$，证明$CD^{2}= BD ×AD$。
- 在$\triangle ABC$中，边$AB$延长到$D$，使得$BD = BC$。如果$\angle B = 60^o$且$\angle A = 70^o$，证明$AD > CD$。
- 在图中，直线$AB$和$CD$相交于$O$。如果$\angle AOC + \angle BOE = 70^o$且$\angle BOD = 40^o$，求$\angle BOE$和$\angle COE$的度数。
- 在图中，四边形$ABCD$被画成外接一个圆，圆心为$O$，使得边$AB,\ BC,\ CD$和$DA$分别与圆相切于点$P,\ Q,\ R$和$S$。证明$AB\ +\ CD\ =\ BC\ +\ DA$。
- 两条直线$AB$和$CD$相交于$O$。如果$\angle AOC + \angle COB + \angle BOD = 270^o$，求$\angle AOC, \angle COB, \angle BOD$和$\angle DOA$的度数。
- 在图中，直线$AB, CD$和$EF$相交于$O$。求$\angle AOC, \angle COF, \angle DOE$和$\angle BOF$的度数。
- $O$是两条相等弦$AB$和$CD$的交点，使得$OB=OD$，则证明$\vartriangle OAC$和$\vartriangle ODB$相似。
- 在图中，已知$AB = CD$且$AD = BC$。证明$\triangle ADC \cong \triangle CBA$。
- $ABC$是一个三角形，其中$\angle B = 2\angle C$，$D$是$BC$上的一点，使得$AD$平分$\angle BAC$且$AB = CD$。证明$\angle BAC = 72^o$。
- $AB, CD$和$EF$是三条共点线，经过点$O$，使得$OF$平分$\angle BOD$。如果$\angle BOF = 35^o$，求$\angle BOC$和$\angle AOD$。
- 在图中，证明：$CD + DA + AB > BC$
- 四边形$ABCD$被画成外接一个圆（见图）。证明$AB + CD = AD + BC$。
数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究