一个四边形 $ABCD$ 外接一个圆（见图）。证明 $AB + CD = AD + BC$。
"

已知：

一个四边形 $ABCD$ 外接一个圆

要求：

我们必须证明 $AB\ +\ CD\ =\ AD\ +\ BC$。

解答

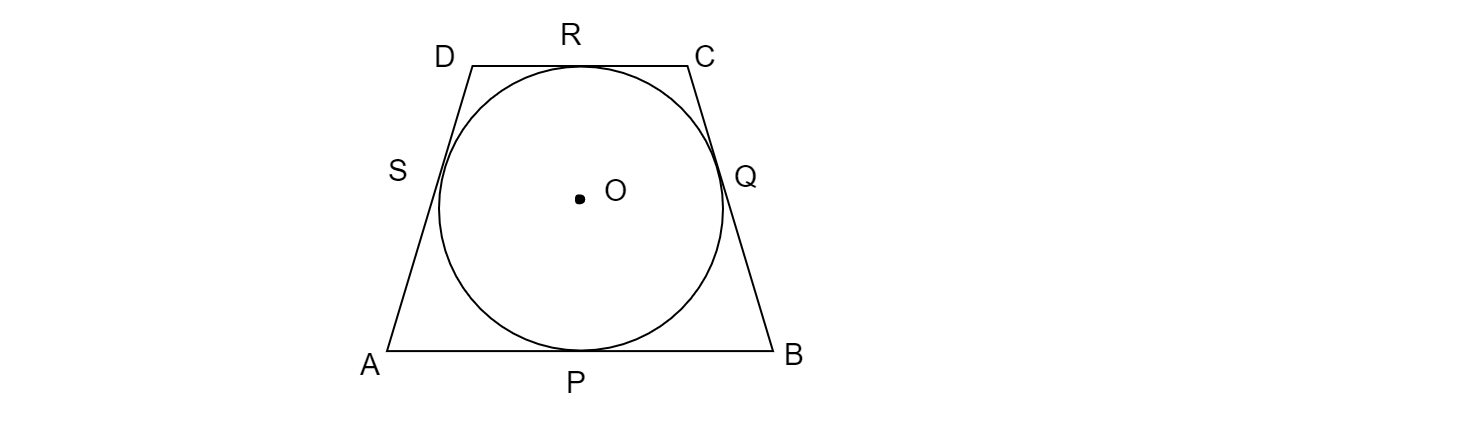
由于从圆外一点引出的切线长度相等，

$AP\ =\ AS\ \dotsc .( 1)$

$BP\ =\ BQ\ \dotsc .( 2)$

$CR\ =\ CQ\ \dotsc .( 3)$

$DR\ =\ DS\ \dotsc .( 4)$

将方程式 $( 1) ,\ ( 2) ,\ ( 3)$ 和 $( 4)$ 相加，得到

$AP\ +\ BP\ +\ CR\ +\ DS\ =\ AS\ +\ BQ\ +\ CQ\ +\ DS$

$\therefore \ ( AP\ +\ BP) \ +\ ( CR\ +\ DR) \ =\ ( AS\ +\ DS) \ +\ ( BQ\ +\ CQ)$

$\therefore \ AB\ +\ CD\ =\ AD\ +\ BC$

证毕。

教程点

更新于: 2022年10月10日

49 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习