数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
正整数 正整数定义为大于零的整数。它们位于水平数轴上零的右侧，大于零和小于负整数。1, 2, 3, .....是正整数。自然数：数字 1, 2, 3, 4, 5, 6, 7, 8, 9 等用于计数。这些计数数字构成自然数集。自然数用于计数（例如“桌上有六枚硬币”）和排序（例如“这是第三大……” 阅读更多
已知：Rahim 吃了披萨的 $\frac{1}{5}$，Raj 吃了剩余披萨的 $\frac{1}{4}$。求：剩余披萨的比例。解：设披萨总量为 1。Rahim 吃的披萨 = $\frac{1}{5}(1) = \frac{1}{5}$ 现在剩下的披萨 = $1 - \frac{1}{5} = \frac{5-1}{5} = \frac{4}{5}$ Raj 吃的剩余披萨 = $\frac{1}{4}(\frac{4}{5}) = \frac{1}{5}$ 剩下的披萨比例 = $1 - \frac{1}{5} - \frac{1}{5} = 1 - \frac{2}{5} = \frac{5-2}{5} = \frac{3}{5}$。剩下的披萨比例是 $\frac{3}{5}$。
已知：表达式为 $[[(- \frac {2}{3})^{-3}]^{-4}]^{-2}$。求解：我们需要计算给定表达式的值。解：我们知道，$[a^m]^n = a^{m\times n}$ $[[(- \frac {2}{3})^{-3}]^{-4}]^{-2} =[(- \frac {2}{3})^{-3}]^{-4 \times -2} = [(- \frac {2}{3})^{-3}]^{8} =(- \frac {2}{3})^{-3\times 8} =(- \frac {2}{3})^{-24}$ 这可以写成：$=(- \frac {3}{2})^{24} = \frac{3^{24}}{2^{24}} = (\frac{3}{2})^{24}$ $[[(- \frac {2}{3})^{-3}]^{-4}]^{-2}$ 的值为 $(\frac{3}{2})^{24}$
已知：$x: 81^{-2} \div 729^{1-x}=9^{2 x}$ 求解：解该表达式。解：$81 = 9^2$ $729 = 9^3$ LHS=$81^{-2} \div 729^{1-x} =(9^2)^{-2} \div (9^3)^{1-x} = 9^{-4} \div 9^{3-3x} = 9^{-4+3x-3}$ RHS = $9^{2x}$ 比较 LHS 和 RHS $3x - 7 = 2x$ $3x - 2x = 7$ $x = 7$ 因此，$x=7$
已知：给定的分数为 $\frac{11}{8} , \frac{17}{12}, \frac{5}{3}, \frac{8}{6} $。求解：我们需要将给定的分数写成带分数，并按升序排列。解：$\frac{11}{8} = \frac{11\times 3}{8\times 3} = \frac{33}{24} =\frac{24+9}{24} = 1\frac {9}{24}$ $\frac{17}{12} = \frac{17\times 2}{12\times 2} = \frac{34}{24} =\frac{24+10}{24} = 1\frac {10}{24}$ $\frac{5}{3} = \frac{5\times 8}{3\times 8} = \frac{40}{24} =\frac{24+16}{24} = 1\frac {16}{24}$ $\frac{8}{6} = \frac{8\times 4}{6\times 4} = \frac{32}{24} =\frac{24+8}{24} = 1\frac {8}{24}$ 比较分数，$1\frac {8}{24} < 1\frac {9}{24}$
已知：数字为 a) 5634 b) 65990。求解：检验给定数字能否被 6 整除。解：6 的整除规则 如果一个数字以 0、2、4、6 或 8 结尾，则它可以被 2 整除。如果一个数字的各位数字之和可以被 3 整除，则该数字可以被 3 整除。如果一个数字同时可以被 2 和 3 整除，则它可以被 6 整除。a) 5634 5634 以 4 结尾。因此，数字 5634 可以被 2 整除。$5 + 6 + 3 + 4 = 18$。18 可以被 3 整除… 阅读更多
解：1331：它介于 $10^3$ = 1000 和 $20^3$ = 8000 之间，其最后一位数字是 1。1 的立方是 1，所以 1331 的立方根 = 11 4913：它介于 $10^3$ = 1000 和 $20^3$ = 8000 之间，其最后一位数字是 3。它是 7 的立方的最后一位数字，所以 4913 的立方根 = 17 12167：它介于 $20^3$ = 8000 和 $30^3$ = 27000 之间，其最后一位数字是 7。它是 3 的立方的最后一位数字，所以 12167 的立方根 = 23
CPCT 指的是全等三角形的对应部分。如果两个三角形全等，则它们的所有对应角和边都必须相等。
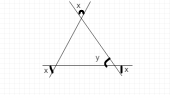
已知：所有外角都相等。求解：我们需要求 x 和 y 的值。解：$∠x = ∠x ; ∠x = ∠y$ （对顶角）三角形的所有三个角都等于∠$x$。因此，根据三角形内角和定理，$∠x + ∠x + ∠x = 180°$ 或 $3∠x = 180°$ 或 $∠x = \frac{180°}{3} = 60°$ $∠x = 60°$ 且 $∠y = 60°$ 选项 b) 各 60° 是正确的。