数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
简单蒸馏和分馏的区别如下：- 简单蒸馏 分馏 1. 用于分离沸点差异足够大的互溶液体的混合物。 1. 当沸点差异很小的时候使用。2. 由一个简单的装置组成，包括一个冷凝器和两个烧瓶。 2. 由一个复杂的装置组成，包括一个分馏柱。 3. 例子：净化海水 3. 例子：原油精炼
已知：Shalina 在一次测试中获得了总分的 $\frac{4}{5}$。测试的总分 = 50。要求：我们必须找到分数。解答：Shalina 获得的分数 = $\frac{4}{5} (50) = 4\times 10 = 40$因此，Shalina 在测试中得了 40 分。
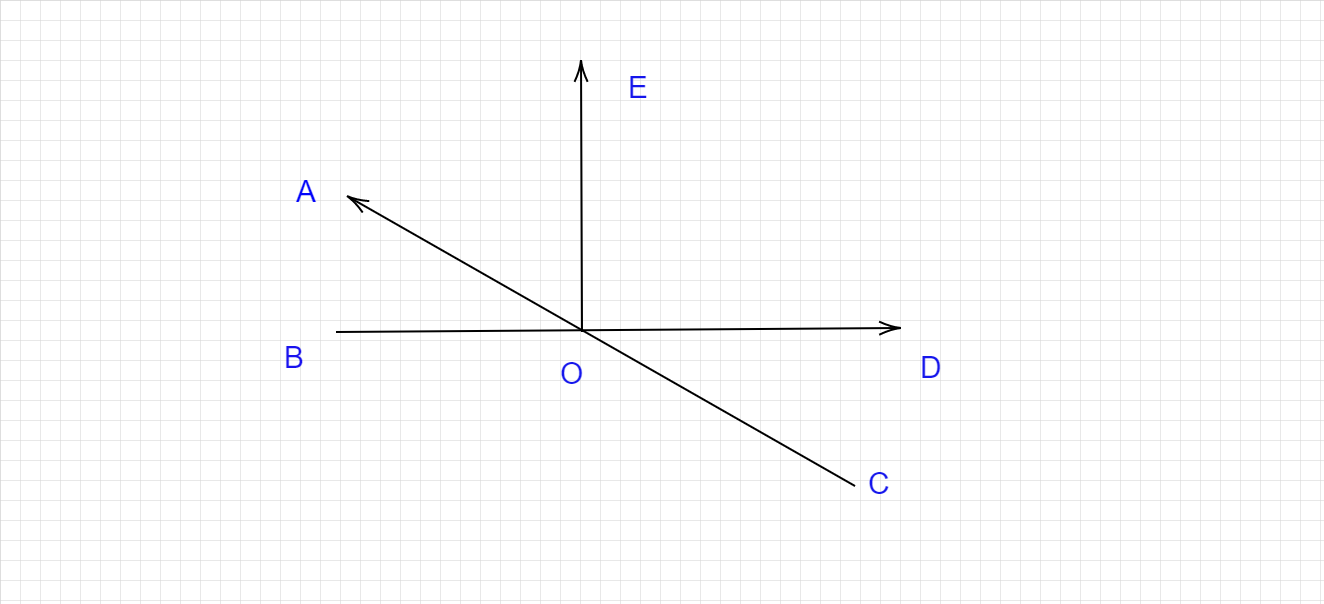
"\已知：给出了相交线的图形。要求：我们必须命名给定的角对。解答：(i) 钝角对顶角是 $∠AOD$ 和 $∠BOC$。(ii) 邻补角是 $∠BOA$ 和 $∠AOE$。(iii) 相等的补角是 $∠AOD + ∠DOC = ∠AOB + ∠BOC, ∠BOA + ∠AOD = ∠BOC + ∠COD$ (iv) 不相等的补角是 $∠BOE + ∠EOD = ∠BOC + ∠COD, ∠AOE + ∠EOC = ∠AOB + ∠BOC$。(v) 不构成线性对的邻角是 $∠AOE$ 和 $∠EOD$； $∠EOD$ 和 $∠DOC$； $∠DOC$ 和 $COB; ∠COB$ 和 $∠BOA; ∠BOE$ 和 $∠EOD$。
欧几里得除法算法：欧几里得除法引理指出，如果存在两个正整数 a 和 b，则存在唯一的整数 q 和 r 满足条件 $a = bq + r$，其中 $0 ≤ r < b$这可以通过以下示例理解：我们知道在任何除法问题中：$被除数 =（除数 × 商）+ 余数$。例如，如果我们将 7 除以 3：被除数 $= 7$除数 $= 3$商 $= 2$余数 $= 1$对于数字 7 和 3，存在数字 2 和 1 使得 $7 = 2 \times 3 + 1$，其中 $0 ≤ 1 < 3$。
已知：给定的分数是 $\frac{65}{177}$。要求：我们必须将 $\frac{65}{177}$ 化简为最简分数。解答：简单分数：当分子和分母都不能再小，同时仍然是整数时，分数就处于最简形式。例如：$\frac{3}{6}$ 可以化简为 $\frac{1}{2}$。要化简分数，请将分子和分母除以可以将这两个数字精确除尽的最大数字。65 的因数是 1、5、13 和 65。177 的因数是 1、3、59 和 177。65 和 177 没有公因数。因此，$\frac{65}{177}$ 已经是最简分数了。312507=104×3169×3=104169=8×1313×13=813\frac{312}{507} =\frac{104\times 3}{169\times ... 阅读更多
已知：溶质体积 = 4.5 cm³ = 4.5 ml溶剂体积 = 125 cm³ = 125 ml要求：溶液的浓度解答：溶液体积 = 溶质体积 + 溶剂体积= 4.5 + 125 = 129.5 ml浓度 = $\frac{溶质体积}{溶液体积} \times 100$= $\frac{4.5}{129.5} \times 100$$= 0.03479 \times 100$= 3.749%
已知：给定的数据是 72、68、42、33、35、39、40、65、69。要求：我们必须找到给定数据的中位数。解答：将数字按升序排列，33、35、39、40、42、65、68、69、72给定数据的中位数是升序排列中的中间数，即 42。因此，给定数据的中位数是 42。
已知：35、10、10、35、45、32、73、90、45、34、12。要求：这里我们必须找到 35、10、10、35、45、32、73、90、45、34、12 的中位数。解答：要找到中位数，我们找到中间的数字。首先，我们将数字按升序排列。给我们的数字是 35、10、10、35、45、32、73、90、45、34 和 12。升序：10、10、12、32、34、35、35、45、45、73、90。当观察值的个数 (n) 为奇数时，中位数是第 $\frac{n\ +\ 1}{2}$ 个观察值的值。这里，n = 11。所以，$\frac{11\ +\ 1}{2} \ =\ \frac{12}{2} \ =$ 第 6 个观察值。第 6 个观察值 = 35所以，给定数据集的中位数是 35。