已知:$(2x-3y)^3+(3y-4z)^3+(4z-2x)^3$。求解:我们需要对给定的表达式进行因式分解。解:$(2x-3y)^3+(3y-4z)^3+(4z-2x)^3$使用公式 $a^3 + b^3 + c^3 = 3abc$,如果 $a+b+c = 0$令 $a =2x-3y; b = 3y - 4z; c = 4z - 2x$$a + b + c = 2x -3y + 3y - 4z + 4z - 2x = 0$$a^3 + b^3 + c^3 = 3abc$所以 $(2x-3y)^3+(3y-4z)^3+(4z-2x)^3 = 3(2x-3y) (3y-4z)(4z-2x)$所以 $(2x-3y)^3+(3y-4z)^3+(4z-2x)^3$ 已如上所示进行因式分解。
已知:给定的多项式为 $x^3 + x^2- 4x - 4$。求解:我们需要对给定的多项式进行因式分解。解:我们知道,$a^2-b^2= (a+b)(a-b)$ $x^3+x^2-4x-4 = x^2 (x+1)-4(x+1)$ $= (x^2-4)(x+1)$ $ =(x^2-2^2)(x+1)$ $= (x+2)(x-2)(x+1)$ 因此,多项式 $x^3 + x^2- 4x - 4$ 的因子为 $(x+1)$、$(x+2)$ 和 $(x-2)$。
已知:给定的多项式为 $x^8 - y^8$。求解:我们需要对给定的多项式进行因式分解。解:我们知道,$a^2 - b^2 = (a+b)(a-b)$ 因此,$x^8 - y^8 =(x^4)^2 - (y^4)^2$ $ = (x^4 + y^4)(x^4 - y^4)$ $= (x^4 + y^4)(x^2)^2 - (y^2)^2$ $ = (x^4 + y^4)(x^2 + y^2)(x^2 - y^2) $ $ = (x^4 + y^4)(x^2 + y^2)(x+y)(x-y)$ 因此,多项式 $x^8 - y^8$ 的因子为 $(x^4 + y^4)(x^2 + y^2)(x+y)$ 和 $(x-y)$
已知:给定的表达式为 $x^3-8y^3-36xy$求解:我们需要在 $x=2y+6$ 时求 $x^3-8y^3-36xy$ 的值。解:$x = 2y+6$$x-2y = 6$两边取三次方,得到 $(x-2y)^3= (6)^3$$x^3-(2y)^3-3(x)(2y)(x-2y) = 216$ $x^3-8y^3-6xy(6) = 216$ $x^3-8y^3-36xy = 216$。$x^3-8y^3-36xy$ 的值为 $216$。
已知:给定的数字是 3528 和 2。求解:我们需要将 3528 除以 2。解:被除数 $= 3528$除数 $= 2$ 1764235282 1514 12 12 8 8--------- 0---------商 $= 1764$余数 $= 0$。3528 除以 2 等于 1764。
已知:1) 475320 2) 95432求解:写出以下数字使用位值表,并写出它们的展开形式。解:1) 475320 的位值表十万万千百十个475320475320 = 4 $\times$ 100000 $+$ 7 $\times$ 10000 $+$ 5 $\times$ 1000 $+$ 3 $\times$100 $+$ 2 $\times$ 10 $+$ 0 $\times$ 1 2) 95432 的位值表万千百十个 95432 95432 = 9 $\times$ 10000 $+$ 5 $\times$ 1000 $+$ 4 $\times$ 100 $+$ 3 $\times$ 10 $+$ 2 $\times$ 1
| 科目 | 英语 | 印地语 | 数学 | 科学 | 社会科学 |
| 第一学期(满分 100 分) | 67 | 72 | 88 | 81 | 73 |
| 第二学期(满分 100 分) | 70 | 65 | 95 | 85 | 75 |
(iii) 哪个科目的成绩下降了?
已知:第一学期英语成绩 $= 67$分第二学期英语成绩 $= 70$分第一学期印地语成绩 $= 72$分第二学期印地语成绩 $= 65$分第一学期数学成绩 $= 88$分第二学期数学成绩 $= 95$分第一学期科学成绩 $= 81$分第二学期科学成绩 $= 85$分第一学期社会科学成绩 $= 73$分第二学期社会科学成绩 $= 75$分求解:我们需要找到,(i) 孩子在哪个... 阅读更多
$ \begin{array}{l}\frac{26^{4} \ \times \ 3^{5} \ \times \ x^{7}}{13^{3} \ \times \ (6x)^{4}}\\\\\\\\=\ \frac{26\ \times \ 26\ \times \ 26\ \times \ 26\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ 3\ \times \ x^{3} \ \times \ x^{4}}{13\ \times \ 13\ \times \ 13\ \times \ 6\ \times \ 6\ \times \ 6\ \times \ 6\ \times \ x^{4}}\\\\\\\\=\ \frac{2\ \times \ 2\ \times \ 2\ \times \ 26\ \times \ 1\ \times \ 1\ \times \ 1\ \times \ 1\ \times \ 3\ \times \ 3\ \times \ x^{3} \ \times \ 1}{1\ \times \ 1\ \times \ 1\ \times \ 2\ \times \ 2\ \times \ 2\ \times \ 2\ \times \ 1}\\\\\\\\=\ \frac{2\ \times \ 2\ \times \ 2\ \times \ 26\ \times \ 3\ \times \ 3\ \times \ x^{3}}{2\ \times \ 2\ \times \ 2\ \times \ 2}\\\\\\=\ \frac{1\ \times \ 1\ \times \ 1\ \times \ 13\ \times \ 3\ \times \ 3\ \times \ x^{3}}{1\ \times \ 1\ \times \ 1\ \times \ 1}\\\\\\=\ \mathbf{117x^{3}}\end{array}$

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
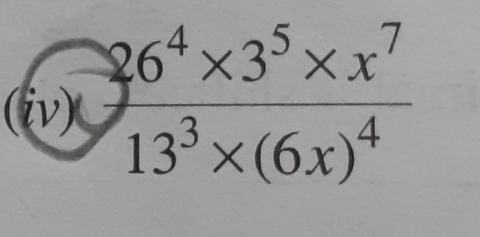 "\
"\