数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：给定的表达式为 $9 ÷ 2 \frac{3}{4}$。需要做：我们需要将给定的表达式表示为最简形式。解答：我们知道，$(\frac{a}{b}) ÷ (\frac{c}{d}) = (\frac{a}{b}) \times (\frac{d}{c})$ $9 ÷ 2 \frac{3}{4} = 9 ÷ \frac{(2\times 4+3)}{4}$ $= 9 ÷ \frac{(8+3)}{4}$ $= \frac{9}{1} ÷\frac{11}{4}$ $= \frac{9}{1} \times \frac{4}{11}$ $= \frac{(9\times 4)}{(1\times 11)}$ $= \frac{36}{11}$ $\frac{36}{11} = \frac{(11\times 3+3)}{11}$ $=3 \frac{3}{11}$ 因此，$9 ÷ 2 \frac{3}{4}$ 的最简形式为 $3 \frac{3}{11}$。
已知：给定的表达式为 $\frac{7}{15} ÷ 3$。需要做：我们需要将给定的表达式表示为最简形式。解答：我们知道，$(\frac{a}{b}) ÷ (\frac{c}{d}) = (\frac{a}{b}) \times (\frac{d}{c})$ $\frac{7}{15} ÷ 3= \frac{7}{15} ÷ \frac{3}{1}$ $= (\frac{7}{15}) \times (\frac{1}{3})$ $= \frac{(7\times1)}{(15\times3)}$ $= \frac{7}{45}$。因此，$\frac{7}{15} ÷ 3$ 的最简形式为 $\frac{7}{45}$。
已知：$3\frac{1}{5}$需要求：我们需要求应该将什么数乘以 $3\frac{1}{5}$，才能使积为 1。解答：$3\frac{1}{5}\ =\ \frac{16}{5}$设所需数字为 = a所以，$\frac{16}{5}\ \times\ a\ =\ 1$$a\ =\ 1\ \times\ \frac{5}{16}$$\mathbf{a\ =\ \frac{5}{16}}$所以，所需数字为 $\frac{5}{16}$。
已知：给定的表达式为 $p(x) = x^2 - 2\sqrt{2}x+1$。需要做：我们需要求 $p(2\sqrt{2})$ 的值。解答：$p(x) = x^2 - 2\sqrt{2}x+1$ $p(2\sqrt{2}) = (2\sqrt{2})^2 - 2\sqrt{2} (2\sqrt{2}) +1$ $= (2\sqrt{2})^2 -(2\sqrt{2})^2 +1 $ $ = 0 + 1 = 1$因此，$p(2\sqrt{2})$ 的值为 1。
已知：1000 卢比由 1 卢比和 2 卢比的硬币组成，其比例为 4:3。需要做：我们需要求 2 卢比硬币的数量。解答：设 1 卢比硬币的数量为 4x，2 卢比硬币的数量为 3x。因此，$Rs. 4x(1) + Rs. 3x(2) = Rs. 1000$$4x+6x = 1000$$10x = 1000$$x = \frac{1000}{10}$$x = 100$1 卢比硬币的数量 $= 4(100) = 400$。2 卢比硬币的数量 $= 3(100) = 300$。因此，2 卢比硬币的数量为 300。
已知：给定的多项式为 $2x+5$。需要做：我们需要求多项式的零点。解答：多项式的零点定义为 x 的任何实数值，使得多项式的值为零。因此，多项式 $p(x) = 2x+5$ 的零点为，$2x+5 = 0$$2x = -5$$x = \frac{-5}{2}$。多项式 $p(x) = 2x+5$ 的零点为 $\frac{-5}{2}$。
如果 a、b、c 成等比数列，则 b2 = acx 、1 、0.5 成等比数列=> 12 = x (0.5)=> x = 2
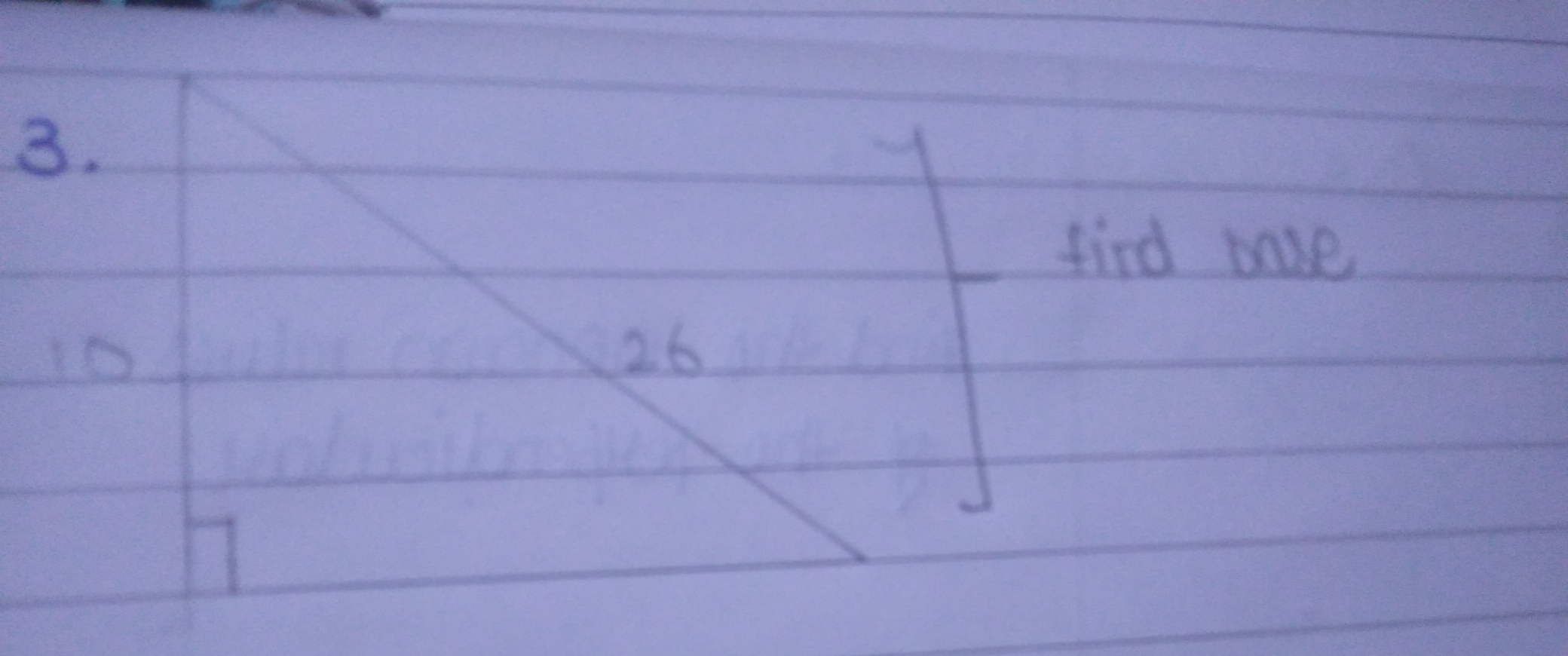
"\嗨，Shubhi，我们可以看到给定的三角形是直角三角形。根据勾股定理底边2 + 高2 = 斜边2 底边2 + 102 = 262 底边2 = 262 - 102 底边 = √(262 - 102) 底边 = 24
已知：一个人以每年 10.5% 的复利（每年支付一次利息）借出 4000 卢比。另一个人以每年 10% 的复利（每半年支付一次利息）借出相同数额的钱。需要做：我们需要求在 1 年 8 个月后，谁赚得更多，以及多赚了多少。解答：一个人以每年 10.5% 的复利（每年支付一次利息）借出 4000 卢比。利息 = 10.5% 时间 = 1 年复利可以通过以下公式计算，... 阅读更多