三千二百零一写成数字是 3021。
已知:给定的表达式是 $-72+(-52)\times51237$求解:我们需要求解给定表达式的值。解答:$-72+(-52)\times51237 = -72 - 52 \times 51237$ $ = -72 - 2664324 = - 2664396$给定表达式 $-72+(-52)\times51237$ 的值为 $-2664396$
对流:当流体(如空气或液体)被加热并远离热源移动时,空气或液体的粒子吸收热量。热表面的粒子膨胀,密度降低,并上升。这种类型的热传递称为对流。这种机制在使用对流烤箱烹饪时使用。在对流烤箱中,风扇在食物周围循环热空气,因此食物比非对流烤箱烹饪得更快。
解答:a)$730 + 998$ 将 730 四舍五入到最接近的百位数,得到 $700$ 将 998 四舍五入到最接近的百位数,得到 $1, 000$ 因此,$700 + 1000 = 1, 700$ 因此,根据一般规则,$730+998$ 的估计值为 $1, 700$。b)$796 – 314$ 将 796 四舍五入到最接近的百位数,得到 $800$ 将 314 四舍五入到最接近的百位数,得到 $300$ 因此,$800 - 300 = 500$ 因此,根据一般规则,$796 – 314$ 的估计值为 $500$。c)$12, 904 +2, 888$将 12, 904 四舍五入到最接近的 ... 阅读更多
如果我们烤烙饼,它将是不可逆变化的一个例子,但如果我们不烤烙饼而留下生面团,那么它也将是不可逆变化的一个例子,因为在这两种情况下,我们都无法恢复原来的成分。
已知:给定的表达式为,a. $342 \times 12 +342 \times 8$b. $6842 \times 999 + 6842$。操作:我们需要使用合适的性质简化给定的项。解答:分配律:乘法的分配律指出,当一个因子乘以两个项的和或差时,必须将这两个数中的每一个都乘以因子,最后执行加法或减法运算。此属性在符号上表示为:$a (b+c) = a\times b + a\times c$$a (b-c) = a\times b - a\times c$a. $342 \times 12 + 342 \times 8$$= 342 \times (12 + ... 阅读更多
液体的压力随液体的深度而变化。相同深度处的液体内部压力将相等。液体在深处的压力与深度成正比(P∝h)。因此,选项 (d) 是正确的,A 处的压力< B 处的压力< C 处的压力。
已知:在一个等腰三角形中,底角相等。顶角为 50°。操作:我们需要找到三角形底角的度数。解答:设每个底角的度数为 x。我们知道,三角形内角和为 180°。因此,$x+x+50° = 180°$$2x = 180°-50°$$2x=130°$$x=\frac{130°}{2}$$x = 65°$因此,每个底角的度数为 65°。
已知:给定的表达式是 $\frac{-16}{7} \times (\frac{-8}{9} + \frac{-7}{6}) = (\frac{-16}{7} \times \frac{-8}{9}) + (\frac{-16}{7} \times \frac{-7}{6})$.操作:我们需要使用合适的性质求解给定的表达式。解答:分配律:乘法的分配律指出,当一个因子乘以两个项的和或差时,必须将这两个数中的每一个都乘以因子,最后执行加法或减法运算。此属性在符号上表示为:$a (b+c) = a\times b + a\times c$$a (b-c) = a\times b - a\times c$$\frac{-16}{7} \times (\frac{-8}{9} + \frac{-7}{6}) = (\frac{-16}{7} \times \frac{-8}{9}) + ... 阅读更多
已知:给定的表达式为,a. $9x + 1$b. $\frac{2}{x} - 1$c. $\frac{1}{b} + 3$。操作:我们需要从给定的表达式中识别多项式。解答:多项式:多项式是指每个项都是一个常数乘以一个变量的整数次幂的表达式。a. 在 $9x+1$ 中,项中的变量 (x) 被提升到整数次幂。b. 在 $\frac{2}{x}-1$ 中,项 $\frac{1}{x}$ 等于 $x^{-1}$,在这个项中,变量 x 被提升到 -1 次幂,这不是一个整数。c. 在 $\frac{1}{b}+3$ 中,项 $\frac{1}{b}$ 等于 $b^{-1}$,并且在 ... 阅读更多

 数据结构
数据结构 网络
网络 RDBMS
RDBMS 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
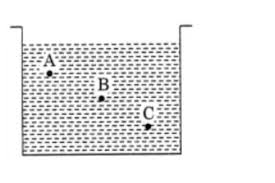 (a) A 处的压力 > B 处的压力 > C 处的压力(b) A 处的压力 = B 处的压力 = C 处的压力(c) A 处的压力 < B 处的压力 < C 处的压力(d) A 处的压力 "\
(a) A 处的压力 > B 处的压力 > C 处的压力(b) A 处的压力 = B 处的压力 = C 处的压力(c) A 处的压力 < B 处的压力 < C 处的压力(d) A 处的压力 "\