交流和电压的平均值和有效值

交流量的平均值

交流量在一个周期内所有瞬时值的算术平均值称为“交流量的平均值”。

$$平均值=\frac{一个周期内所有瞬时值的和}{瞬时值的个数}$$

$$=\frac{时间周期T内曲线下的总面积}{时间周期(T)}$$

$$=\frac{i_{1}+i_{2}+i_{3}+...+i_{n}}{n}$$

对称波形的平均值

对于像正弦电压或电流这样的对称波形，在一个周期内的平均值为零。这是因为正半周期与负半周期完全相等。但正半周期或负半周期的平均值不为零。因此，对于对称波形，平均值是在半个周期内计算的。

$$平均值 = \frac{半个周期内所有瞬时值的和}{半个周期内瞬时值的个数}$$

非对称波形的平均值

对于像半波整流电压这样的非对称波形，平均值是在整个周期内计算的。

$$平均值 = \frac{半个周期内所有瞬时值的和}{一个周期内瞬时值的个数}$$

由于正弦交流电压和电流在全世界范围内得到了最广泛的应用。因此，我们找到正弦电压和电流的平均值和有效值。

正弦电压或电流的平均值

交流（正弦电压或电流）的平均值是直流的值，该值在半个周期内通过电路发送的电荷量与交流在相同时间内通过相同电路发送的电荷量相同。它用 I_av 表示。

正弦交流电压或电流在一个周期内的平均值为零。这是因为正半周期的面积与负半周期的面积完全相等。但是，在半个周期（正或负）内的平均值不为零。因此，正弦电压或电流的平均值是指半个周期的平均值。

推导 – 交流的平均值可以通过将电流或电压的瞬时值在半个周期内积分（即半个周期内曲线的面积）并将结果除以半个周期的基长来获得。

$$平均值=\frac{半个周期内的面积}{半个周期的基长}$$

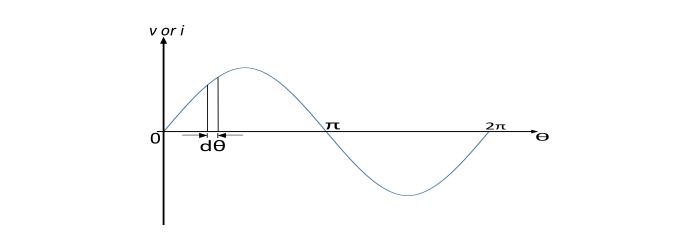
正弦变化电压的方程由下式给出

$$u=V_{m}\sin\theta$$

让我们在波形的正半周期内取一个厚度为 dθ 的条带。考虑 v 为条带的平均高度。因此，

$$条带的面积= u\:d\theta$$

$$半个周期的面积=\int_{0}^{\pi} u\:\sin\theta\:d\theta$$

$$=V_{m}[-\cos\theta]_0^\pi=2V_{m}$$

$$平均值(V_{a u})=\frac{半个周期的面积}{半个周期的基长}=\frac{2V_{m}}{\pi}=0.637V_{m}$$

类似地，对于正弦交流电流，

$$平均值(I_{a u})=\frac{半个周期的面积}{半个周期的基长}=\frac{2l_{m}}{\pi}=0.637l_{m}$$

因此，正弦交流电流或电压的平均值等于最大值或峰值的 0.637 倍。

正弦电压或电流的有效值

正弦交流电流（AC）的均方根 (RMS) 或有效值是直流的值，当其在给定时间内流过给定电阻时，产生的热量与交流在相同时间内流过相同电阻时产生的热量相同。

有效值 = 电流的平方均值的平方根

$$交流电流的有效值(𝐼) =\sqrt{i^{2}的平均值}=\sqrt{\frac{i_{1}^{2}+i_{2}^{2}+i_{3}^{2}+...+i_{n}^{2}}{n}}$$

类似地，交流电压的有效值可以表示为 -

$$交流电压的有效值( u) =\sqrt{ u^{2}的平均值}=\sqrt{\frac{ u_{1}^{2}+ u_{2}^{2}+ u_{3}^{2}+...+ u_{n}^{2}}{n}}$$

• 对于对称波形，有效值可以通过考虑半个周期或整个周期来计算。但是，对于非对称波形，应考虑整个周期。

• 对于对称波，

$$有效值=\sqrt{\frac{半个周期平方波的面积}{半个周期的基长}}$$

正弦电流或电压的有效值

由于正弦波是对称波。因此，我们可以通过仅考虑半个周期来计算其有效值。

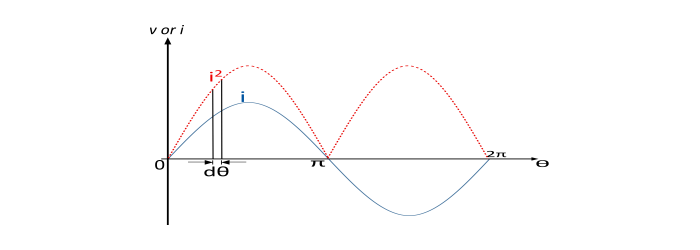
正弦交流电流的方程由下式给出

$$i=I_{m}\sin\theta$$

让我们考虑在平方电流波（显示为红色虚线）的正半周期内取一个宽度为 dθ 的条带。设 i² 为条带的平均高度。

$$条带的面积=i^{2}\:d\theta$$

$$平方波半个周期的面积=\int_{0}^{\pi}i^{2}\:d\theta=\int_{0}^{\pi}I_{m}^{2}\sin^{2}\theta\:d\theta$$

$$=I_{m}^{2}\int_{0}^{\pi}\sin^{2}\theta\:d\theta=\frac{\pi\:I^{2}m}{2}$$

因此，

$$I_{RMS}=\sqrt{\frac{平方波半个周期的面积}{半个周期的基长}}=\sqrt{\frac{{\pi\:I_{m}^{2}}/{2}}{\pi}}=\frac{I_{m}}{\sqrt{2}}=0.707I_{m}$$

类似地，正弦交流电压的有效值为

$$V_{RMS}=\frac{V_{m}}{\sqrt{2}}=0.707V_{m}$$

因此，正弦交流电压或电流的有效值等于峰值的 0.707 倍。

数值示例 #1

一个正弦电流的最大值为 650 mA。它的平均值是多少？

解决方案

正弦交流电流的平均值由下式给出

$$I_{a u}=\frac{2I_{m}}{\pi}=0.637I_{m}$$

$$I_{a u}=0.637 × 650 ×\:10^{-3}=414.05mA$$

数值示例 #2

交流电压的方程由 ν = 325.22 𝑠𝑖𝑛314𝑡 给出。求 (i) 有效值 (ii) 频率 (iii) 平均值。

解决方案

电压的最大值为

$$V_{m}=325.22 V$$

• 电压的有效值

$$V_{RMS}=0.707𝑉𝑚 = 0.707 × 325.22 = 230 V$$

• 频率

$$\because\:\omega= 2𝜋𝑓 = 31$$

$$\therefore\:f=\frac{\omega}{2\pi}=\frac{314}{2\pi}=50 Hz$$

• 平均值

$$V_{a u}=0.637𝑉𝑚 = 0.637 × 325.22 = 207.2 V$$

Saini Manish Kumar

更新于：2021年6月10日

36K+ 次查看

启动您的 职业生涯

通过完成课程获得认证

开始