电阻的电路连接

---

---

当电阻连接到电路中时，该连接可以是串联或并联。现在让我们了解一下，如果它们串联连接以及并联连接时，总电流、电压和电阻值将发生什么变化。

串联电阻

让我们观察一下，当几个电阻串联连接时会发生什么。让我们考虑三个不同值的电阻，如下图所示。

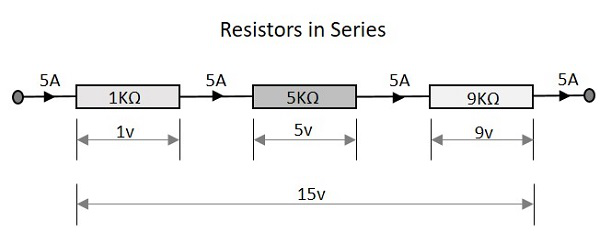
电阻

具有串联电阻的电路的总电阻等于各个电阻的总和。这意味着，在上图中，有三个电阻，其值分别为 1KΩ、5KΩ 和 9KΩ。

电阻网络的总电阻值为 -

$$R\:\:=\:\:R_{1}\:+\:R_{2}\:+\:R_{3}$$

这意味着 1 + 5 + 9 = 15KΩ 是总电阻。

其中 R₁ 是第一个电阻的电阻，R₂ 是第二个电阻的电阻，R₃ 是上述电阻网络中第三个电阻的电阻。

电压

出现在串联电阻网络两端的总电压是每个电阻电压降的总和。在上图中，我们有三个不同的电阻，每个阶段都有三个不同的电压降值。

出现在电路两端的总电压 -

$$V\:\:=\:\:V_{1}\:+\:V_{2}\:+\:V_{3}$$

这意味着 1v + 5v + 9v = 15v 是总电压。

其中 V₁ 是第一个电阻的电压降，V₂ 是第二个电阻的电压降，V₃ 是上述电阻网络中第三个电阻的电压降。

电流

流过一组串联连接的电阻的总电流在整个电阻网络中的所有点都相同。因此，在输入端或电阻之间的任何点，甚至在输出端测量时，电流都相同，为 5A。

通过网络的电流 -

$$I\:\:=\:\:I_{1}\:=\:I_{2}\:=\:I_{3}$$

这意味着所有点的电流都是 5A。

其中 I₁ 是流过第一个电阻的电流，I₂ 是流过第二个电阻的电流，I₃ 是上述电阻网络中流过第三个电阻的电流。

并联电阻

让我们观察一下，当几个电阻并联连接时会发生什么。让我们考虑三个不同值的电阻，如下图所示。

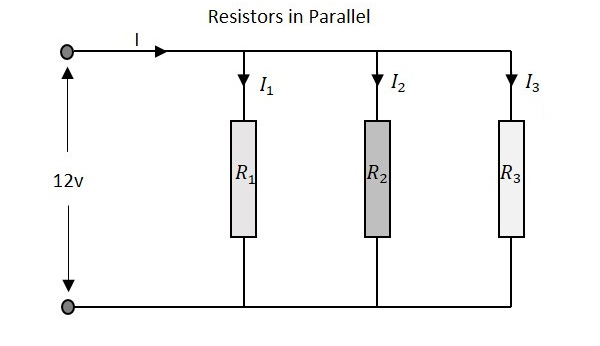
电阻

具有并联电阻的电路的总电阻的计算方法与串联电阻网络方法不同。在这里，将各个电阻的倒数 (1/R) 值与代数和的倒数相加，以获得总电阻值。

电阻网络的总电阻值为 -

$$\frac{1}{R}\:\:=\:\:\frac{1}{R_{1}}\:\:+\:\:\frac{1}{R_{2}}\:\:+\frac{1}{R_{3}}$$

其中 R₁ 是第一个电阻的电阻，R₂ 是第二个电阻的电阻，R₃ 是上述电阻网络中第三个电阻的电阻。

例如，如果考虑前面示例中的电阻值，这意味着 R₁ = 1KΩ，R₂ = 5KΩ 和 R₃ = 9KΩ。并联电阻网络的总电阻将为 -

$$\frac{1}{R}\:\:=\:\:\frac{1}{1}\:\:+\:\:\frac{1}{5}\:\:+\frac{1}{9}$$

$$=\:\:\frac{45\:\:+\:\:9\:\:+\:\:5}{45}\:\:=\:\:\frac{59}{45}$$

$$R\:\:=\:\:\frac{45}{59}\:\:=\:\:0.762K\Omega\:\:=\:\:76.2\Omega$$

根据我们计算并联电阻的方法，我们可以推导出一个用于双电阻并联网络的简单方程。它是 -

$$R\:\:=\:\:\frac{R_{1}\:\:\times\:\:R_{2}}{R_{1}\:\:+\:\:R_{2}}\:$$

电压

出现在并联电阻网络两端的总电压与每个电阻的电压降相同。

出现在电路两端的电压 -

$$V\:\:=\:\:V_{1}\:=\:V_{2}\:=\:V_{3}$$

其中 V₁ 是第一个电阻的电压降，V₂ 是第二个电阻的电压降，V₃ 是上述电阻网络中第三个电阻的电压降。因此，电压在并联电阻网络的所有点都相同。

电流

进入并联电阻网络的总电流是所有并联支路中流过的所有各个电流的总和。每个支路的电阻值决定了流过它的电流值。通过网络的总电流为

$$I\:\:=\:\:I_{1}\:+\:I_{2}\:+\:I_{3}$$

其中 I₁ 是流过第一个电阻的电流，I₂ 是流过第二个电阻的电流，I₃ 是上述电阻网络中流过第三个电阻的电流。因此，不同支路中各个电流的总和得到并联电阻网络中的总电流。

电阻通常用作许多电路输出端的负载。如果根本不使用电阻负载，则在负载前放置一个电阻。电阻通常是任何电路中的基本组件。