基础电子学 - 霍尔效应

---

---

霍尔效应以其发现者埃德温·霍尔命名。这有点类似于弗莱明右手定则。当载流导体I置于横向磁场B中时，会在导体中感应出垂直于I和B的电场E。这种现象称为霍尔效应。

解释

当载流导体置于横向磁场中时，该磁场会对电子施加一定的压力，使电子沿着弯曲的路径继续运动。以下图显示了施加能量的导体。磁场也已标出。

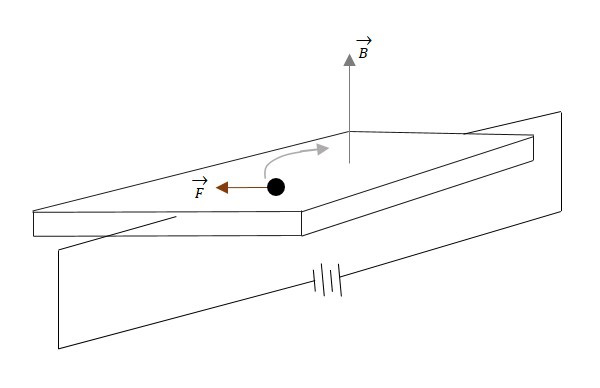
当电子穿过位于磁场B中的导体时，电子将受到磁力。这种磁力会导致电子比另一侧更靠近一侧运动。这在一侧产生负电荷，在另一侧产生正电荷，如下图所示。

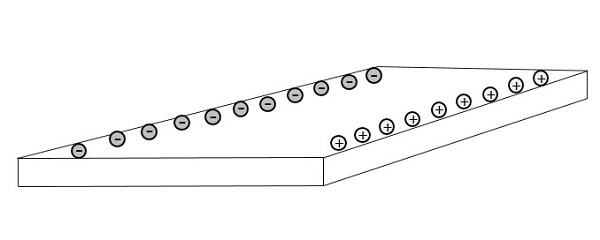
这种电荷分离会产生电压差，称为霍尔电压或霍尔电动势。电压会累积，直到电场对电荷产生的电力与磁力相等且方向相反。这种效应称为霍尔效应。

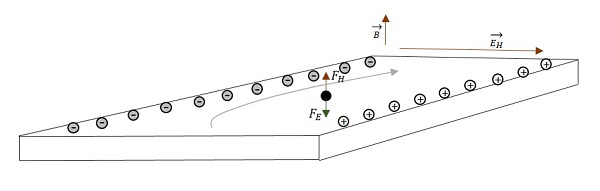
$$\overrightarrow{F_{magnetic}}\:\:=\:\:\overrightarrow{F_{Electric}}\:\:=\:\:q\:\:\overrightarrow{V_{D}}\:\:\overrightarrow{B}\:\:=\:\:q\:\:\overrightarrow{E_{H}}$$

V_D是每个电子所经历的速度

$\overrightarrow{E_{H}}\:\:=\:\:\overrightarrow{V_{D}}\:\:\overrightarrow{B}\:\:$ 因为V = Ed

其中q = 电荷量

$\overrightarrow{B}$ = 磁场

$\overrightarrow{V_{D}}$ = 漂移速度

$\overrightarrow{E_{H}}$ = 霍尔电场

d = 导体中平面之间的距离（导体的宽度）

$$V_{H}\:\:=\:\:\varepsilon_{H}\:\:=\:\:\overrightarrow{E_{H}}\:\:d\:\:=\:\:\overrightarrow{V_{D}}\:\:\overrightarrow{B}\:\:d$$

$$\varepsilon_{H}\:\:=\:\:\overrightarrow{V_{D}}\:\:\overrightarrow{B}\:\:d$$

这是霍尔电动势

用途

霍尔效应用于获取有关半导体类型、载流子符号、测量电子或空穴浓度以及迁移率的信息。由此，我们还可以知道材料是导体、绝缘体还是半导体。它还用于测量磁通密度和电磁波中的功率。

电流类型

谈到半导体中的电流类型，需要讨论两个术语。它们是扩散电流和漂移电流。

扩散电流

掺杂后，电子和空穴的浓度会发生差异。这些电子和空穴倾向于从较高的电荷密度浓度扩散到较低的浓度水平。由于它们是载流子，因此它们构成称为扩散电流的电流。

为了详细了解这一点，让我们考虑N型材料和P型材料。

• N型材料以电子作为多数载流子，以少量空穴作为少数载流子。

• P型材料以空穴作为多数载流子，以少量电子作为少数载流子。

如果将这两种材料彼此靠近连接，则N型材料价带中的一些电子会倾向于向P型材料移动，而P型材料价带中的一些空穴会倾向于向N型材料移动。这两种材料之间发生这种扩散的区域称为耗尽区。

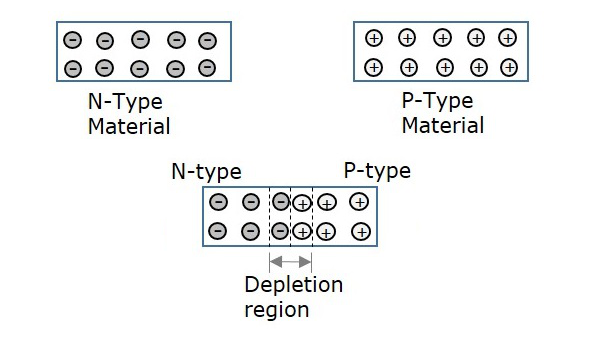
因此，在没有任何外部能量施加的情况下，由于这些电子和空穴的扩散而形成的电流可以称为扩散电流。

漂移电流

由于施加的电场导致带电粒子（电子或空穴）的漂移（运动）而形成的电流称为漂移电流。下图解释了漂移电流，即施加的电场如何产生差异。

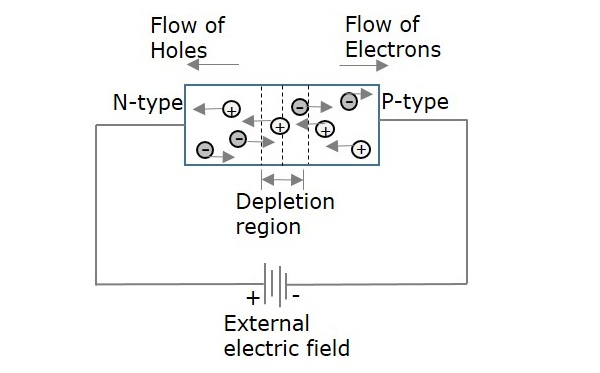
电流的大小取决于施加的电荷。耗尽区的宽度也受到这种漂移电流的影响。为了使组件在有源电路中发挥作用，这种漂移电流起着重要作用。