
- 基础电子学教程
- 基础电子学 - 首页
- 电感器
- 基础电子学 - 电感器
- 基础电子学 - 电感
- 电感器的电路连接
- 电感器的类型
- 基础电子学 - 射频电感器
- 基础电子学有用资源
- 基础电子学 - 快速指南
- 基础电子学 - 有用资源
- 基础电子学 - 讨论
基础电子学 - 电感
电感具有由于电流变化而产生感应电压的特性,这种特性称为电感。电感是电压与电流变化率之比。
电流的变化会产生磁场的变化,磁场的变化会在与电源相反的方向上感应出电动势。这种感应电动势的特性称为**电感**。
电感的公式为
$$电感\:\:=\:\:\frac{电压}{电流变化率}$$
单位 -
电感的单位是**亨利**。用**L**表示。
电感器大多以mH(毫亨利)和μH(微亨利)为单位。
当线圈中自感电动势为**1伏特**,且电流变化率为**每秒1安培**时,则该线圈的电感为**1亨利**。
自感
如果考虑一个有电流流过的线圈,它会产生垂直于电流方向的磁场。当电流持续变化时,磁场也会发生变化,这个变化的磁场会在与电源相反的方向上感应出电动势。产生的这种相反的电动势称为**自感电压**,这种现象称为**自感**。
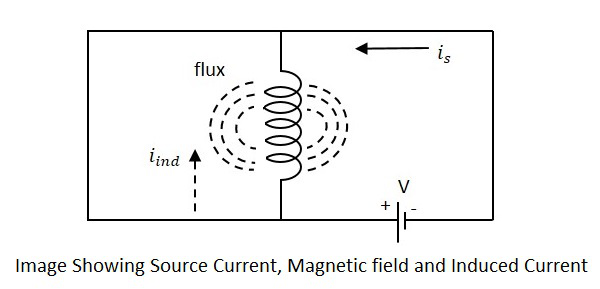
图中的电流is表示电源电流,而iind表示感应电流。磁通量表示线圈周围产生的磁通量。施加电压后,电流is流动并产生磁通量。当电流is变化时,磁通量也会发生变化,从而产生iind。
线圈上的这种感应电动势与电流变化率成正比。电流变化率越高,感应电动势的值越高。
我们可以将上述方程写成
$$E\:\:\alpha\:\:\frac{dI}{dt}$$
$$E\:\:=\:\:L\:\:\frac{dI}{dt}$$
其中,
E是产生的电动势
dI/dt表示电流变化率
L表示电感系数。
自感或自感系数可以表示为
$$L\:\:=\:\:\frac{E}{\frac{dI}{dt}}$$
实际方程写成
$$E\:\:=\:\:-L\:\:\frac{dI}{dt}$$
上述方程中的负号表示根据楞次定律,**感应电动势的方向与电源电压方向相反**。
互感
由于载流线圈在其周围产生磁场,如果将另一个线圈靠近该线圈,使得它位于初级线圈的磁通量区域,那么变化的磁通量会在第二个线圈中感应出电动势。如果第一个线圈称为**初级线圈**,则第二个线圈可以称为**次级线圈**。
当由于初级线圈变化的磁场在次级线圈中感应出电动势时,这种现象称为**互感**。
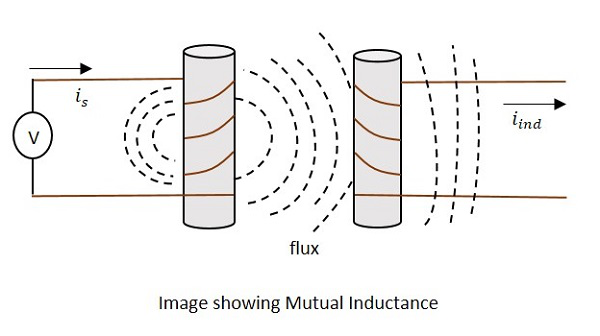
图中的电流is表示电源电流,而iind表示感应电流。磁通量表示线圈周围产生的磁通量。它也扩展到次级线圈。
施加电压后,电流is流动并产生磁通量。当电流is变化时,磁通量也会发生变化,由于互感特性,在次级线圈中产生iind。
变化过程如下。
$$V_{p}\:\:I_{p}\rightarrow\:\:B\:\:\rightarrow\:\:V_{s}\:\:I_{s}$$
其中,
Vp ip分别表示初级线圈的电压和电流
B表示磁通量
Vs is分别表示次级线圈的电压和电流
两个电路的互感M描述了次级线圈中感应电压的大小,该电压由初级线圈电流的变化引起。
$$V(次级)\:\:=\:\:-M\frac{\Delta I}{\Delta t}$$
其中$\frac{\Delta I}{\Delta t}$是电流随时间的变化率,M是互感系数。负号表示电流方向与电源方向相反。
单位 -
互感的单位为
$$伏特\:\:=\:\:M\frac{安培}{秒}$$
(根据上述方程)
$$M\:\:=\:\:\frac{伏特·秒}{安培}$$
$$=\:\:亨利(H)$$
根据初级和次级线圈的匝数,磁通链和感应电动势的大小会发生变化。初级匝数用N1表示,次级匝数用N2表示。耦合系数是一个指定两个线圈互感的术语。
影响电感量的因素
有一些因素会影响电感器的性能。下面讨论主要因素。
线圈长度
电感线圈的长度与线圈的电感成反比。如果线圈长度越长,电感器提供的电感越小,反之亦然。
线圈横截面积
线圈的横截面积与线圈的电感成正比。线圈面积越大,电感越大。
匝数
线圈匝数直接影响电感。电感值与线圈匝数的平方成正比。因此,匝数越多,电感值越大。
磁芯的磁导率
电感器磁芯材料的**磁导率(μ)**表示磁芯自身支持形成磁场的能力。磁芯材料的**磁导率越高**,电感**越大**。
耦合系数
这是计算两个线圈互感的重要因素。让我们考虑两个靠近的线圈,分别为N1和N2匝。
第一线圈中的电流i1产生一些磁通量Ψ1。磁通链的数量用韦伯匝数来理解。
设由于i1的单位电流而产生的第二线圈的磁通链数量为
$$\frac{N_{2}\varphi_{1}}{i_{1}}$$
这可以理解为互感系数,这意味着
$$M\:\:=\:\:\frac{N_{2}\varphi_{1}}{i_{1}}$$
因此,两个线圈或电路之间的互感系数可以理解为一个线圈中由于另一个线圈中1A电流而产生的韦伯匝数。
如果第一个线圈的自感为L1,则
$$L_{1}i_{1}\:\:=\:\:{N_{1}\varphi_{1}}\:\:=>\:\:\frac{L_{1}}{N_{1}}\:\:\frac{\varphi_{1}}{i_{1}}$$
$$M\:\:=\:\:\frac{N_{2}L_{1}}{N_{1}}$$
类似地,由于第二个线圈中电流i2引起的互感系数为
$$M\:\:=\:\:\frac{N_{1}\varphi_{2}}{i_{2}}\:\dotsm\:\dotsm\:\dotsm\:\dotsm\:\:1$$
如果第二个线圈的自感为L2
$$L_{2}i_{2}\:\:=\:\:N_{2}\varphi_{2}$$
$$\frac{L_{2}}{N_{2}}\:\:=\:\:\frac{\varphi_{2}}{i_{2}}$$
因此,
$$M\:\:=\:\:\frac{N_{1}L_{2}}{N_{2}}\:\dotsm\:\dotsm\:\dotsm\:\dotsm\:\:2$$
将1和2相乘,得到
$$M\:\:\times\:\:M=\:\:\frac{N_{2}L_{1}}{N_{1}}\:\:\times\:\:\frac{N_{1}L_{2}}{N_{2}}$$
$$M^{2}\:\:=\:\:L_{1}L_{2}\:\:=>\:\:M\:\:=\:\:\sqrt{L_{1}L_{2}}$$
上述方程在初级线圈的全部变化磁通与次级线圈相连时成立,这是一种理想情况。但在实践中,情况并非如此。因此,我们可以写成
$$M\:\:\neq\:\:\sqrt{L_{1}L_{2}}$$
$$and \frac{M}{\sqrt{L_{1}L_{2}}}\:\:=\:\:K\:\:\neq\:\:1$$
其中K称为耦合系数。
**耦合系数K**可以定义为实际互感系数与理想(最大)互感系数之比。
如果k的值接近于1,则称线圈紧密耦合;如果k=0,则称线圈松散耦合。
电感器的应用
电感器有很多应用,例如 -
电感器用于滤波器电路以检测高频分量并抑制噪声信号
隔离电路不受不需要的高频信号干扰。
电感器用于电子电路中形成变压器,并隔离电路中的尖峰。
电感器也用于电机。