双射函数

---

介绍

双射函数是一一映射且满射的函数。在本教程中，我们将学习函数及其属性，例如单射性和满射性。我们还将学习双射函数以及函数的可逆性。

函数定义为两个集合之间的映射，第一个集合称为定义域，第二个集合称为值域，如果定义域的元素在值域中具有唯一的像。

如果定义域的所有元素都映射到值域中的唯一元素，则称函数为单射或一一映射。如果值域的所有元素都从定义域的某些元素映射而来，则称函数为满射或到映射。如果一个函数既是单射又是满射，则称其为双射。双射函数也是可逆的。

函数

函数定义为两个集合（例如 A 和 B）之间的映射，使得 A 的每个元素在 B 中都有一个唯一的像，即 B 中的任何两个元素都不能映射自 A 的同一个元素。

$$\mathrm{f\:\colon\:a\:\rightarrow\:B\:\:\:\:\:使得\:f(x)\:=\:y}$$

$$\mathrm{其中\:,\:x\;\varepsilon\:A\:,\:y\varepsilon\:B}$$

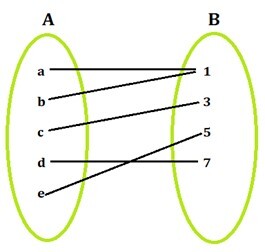
单射性（一一映射）

函数的单射性定义为函数的属性，使得 A 的任何两个元素都不能映射到 B 的同一个元素，即 B 的每个元素都有一个唯一的原像。

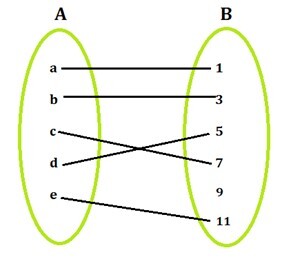
在代数上，函数𝑓的单射性可以通过以下简单方法验证。设$\mathrm{f\:\colon\:A\rightarrow\:B}$为一个函数，

首先，我们将尝试找到一个反例，即定义域中的两个元素映射到值域中的同一个元素。如果没有找到简单的反例，

那么设$\mathrm{x_{1}\:,\:x_{2}\:\varepsilon\:A}$为定义域中的两个元素，它们映射到B中的同一个像，

$$\mathrm{即，f(x_{1})\:=\:f(x_{2})}$$

现在，我们将简化方程并尝试将变量分隔到等式两边。

如果方程可以简化为$\mathrm{x_{1}\:=\:x_{2}}$，则函数𝑓是单射的；但如果存在其他可能成立的条件，则函数𝑓是多对一的，或者简单地说，不是单射的。

满射性（到映射）

函数的满射性定义为函数的属性，使得 B 的所有元素都从 A 的某些元素映射而来，即 B 的所有元素在 A 中都有原像。

它也可以定义为函数的值域等于其值域的时候。

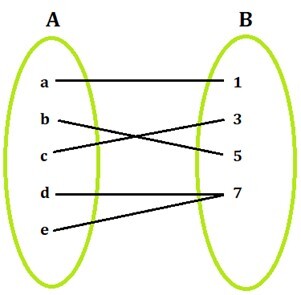
在代数上，函数𝑓的满射性可以通过以下简单步骤确定：

设$\mathrm{f\:\colon\:A\rightarrow\:B;\:f(x)\:=\:y}$

首先，我们将尝试找到一个反例，其中对于某些$\mathrm{y\varepsilon\:B}$，不存在$\mathrm{x\varepsilon\:A}$，使得$\mathrm{f(x)\:=\:y}$。如果没有找到简单的反例，

那么我们将函数表达式代入方程$\mathrm{f(x)\:=\:y}$，并将𝑥与方程的其余部分分离。

这将得到一个函数，例如𝑔，使得

$$\mathrm{g\colon\:B\:\rightarrow\:A;\:g(y)\:=\:x}$$

那么，如果$\mathrm{x\:=\:g(x)\:\varepsilon\:A\:,\:∀\:y\:\varepsilon\:B }$，则函数𝑓是满射的。否则，函数𝑓是入射的，或者简单地说，不是满射的。

双射函数

当一个函数既是单射又是满射时，它被称为双射函数。

可逆性

函数的可逆性由函数复合运算定义。

函数的可逆性取决于其双射性，即如果一个函数是双射的，那么它也是可逆的。

函数𝑓的逆函数$\mathrm{f^{-1}}$，由$\mathrm{f\colon\:A\rightarrow\:B;\:\:f(A)\:=\:B}$定义，定义为：

$$\mathrm{f^{-1}\:\colon\:B\rightarrow\:A;\:f^{-1}(B)\:=\:A}$$

并且，设I为恒等函数，定义为$\mathrm{I\colon\:A\rightarrow\:A;\:\:I(x)\:=\:x\:,\:∀\:x\varepsilon\:A}$

那么，

$$\mathrm{fof^{-1}(B)\:=\:B\:且\:f^{-1}of\:(A)\:=\:A}$$

例题

1) 设𝑓为定义如下函数：$\mathrm{f\colon\:N\rightarrow\:N;\:f(x)\:=\:x^{2}}$。检查𝑓是否是双射的。如果𝑓是双射的，则找到它的逆函数。

答案 - 单射性 -

设，$\mathrm{x_{1}\:,\:x_{2}\:\varepsilon\:N}$

使得，$\mathrm{f(x_{1})\:=\:f(x_{2})}$

$$\mathrm{\Longrightarrow\:{x_{1}}^{2}\:=\:{x_{2}}^{2}}$$

$$\mathrm{\Longrightarrow\:x_{1}\:=\:\pm\:x_{2}}$$

由于集合是自然数集，没有负数，

$$\mathrm{\Longrightarrow\:x_{1}\:=\:x_{2}}$$

因此，该函数是单射的。满射性 -

我们有一个反例，设$\mathrm{y\:=\:2\:\varepsilon\:N}$（值域）不存在任何$\mathrm{x\varepsilon\:N}$（定义域），使得$\mathrm{y\:=\:f(x)\:=\:x^{2}}$

因此，该函数不是满射的，根据定义也不是双射的。

结论

函数定义为两个集合之间的映射，第一个集合称为定义域，第二个集合称为值域，如果定义域的元素在值域中具有唯一的像。如果定义域的所有元素都映射到值域中的唯一元素，则称函数为单射或一一映射。如果值域的所有元素都从定义域的某些元素映射而来，则称函数为满射或到映射。如果一个函数既是单射又是满射，则称其为双射。双射函数也是可逆的。

常见问题

1. 什么是函数？

函数定义为两个集合（例如 A 和 B）之间的映射，使得 A 的每个元素在 B 中都有一个唯一的像，即 B 中的任何两个元素都不能映射自 A 的同一个元素。

$$\mathrm{f\colon\:A\rightarrow\:B\:\:\:\:\:使得\:f(x)\:=\:y}$$

$$\mathrm{其中\:,\:x\:\varepsilon\:A\:,\:且\:y\:\varepsilon\:B}$$

2. 什么是单射函数？

如果定义域的每个元素都映射到值域中的唯一元素，则称函数为单射函数。

3. 什么是满射函数？

如果函数的值域等于其值域，则称函数为满射函数。

4. 双射函数是什么意思？

当一个函数既是单射又是满射时，它被称为双射函数。

5. 如何定义函数的逆函数？

函数𝑓的逆函数𝑓−1，由$\mathrm{f\colon\:A\:\rightarrow\:B;\:\:f(A)\:=\:B}$定义，定义为：

$$\mathrm{f^{-1}\colon\:B\rightarrow\:A;\:f^{-1}(B)\:=\:A}$$

并且，设I为恒等函数，定义为$\mathrm{fof^{-1}(B)\:\:=\:B\:且\:f^{-1}of(A)\:=\:A}$，那么，

$$\mathrm{}$$

6. 如何验证函数的单射性和满射性？

单射性 - 函数𝑓的单射性可以通过以下简单方法验证。设$\mathrm{f\colon\:A\rightarrow\:B}$为一个函数，

首先，我们将尝试找到一个反例，即定义域中的两个元素映射到值域中的同一个元素。如果没有找到简单的反例，

那么设$\mathrm{X_{1},X_{2}\varepsilon\:A}$为定义域中的两个元素，它们映射到B中的同一个像，即，𝑓(𝑥1) = 𝑓(𝑥2)

现在，我们将简化方程并尝试将变量分隔到等式两边。如果方程可以简化为$\mathrm{x_{1}\:=\:x_{2}}$，则函数𝑓是单射的。

满射性 - 函数𝑓的满射性可以通过以下简单步骤确定：

设$\mathrm{f\colon\:A\rightarrow\:B;\:f(x)\:=\:y}$

首先，我们将尝试找到一个反例，其中对于某些$\mathrm{y\varepsilon\:B}$，不存在$\mathrm{x\varepsilon\:A}$，使得$\mathrm{f(x)\:=\:y}$。如果没有找到简单的反例，

那么我们将函数表达式代入方程，并将𝑥与方程的其余部分分离。

这将得到一个函数，例如𝑔，使得：

$$\mathrm{}$$

那么，如果$\mathrm{x\:=\:g(x)\:\varepsilon\:A\:,\:∀\:y\:\varepsilon\:B}$，则函数𝑓是满射的。