计算机图形学 - 二维变换

变换意味着通过应用规则将某些图形更改为其他内容。我们可以进行各种类型的变换，例如平移、缩放（放大或缩小）、旋转、剪切等。当变换发生在二维平面上时，称为二维变换。

变换在计算机图形学中起着重要作用，用于重新定位屏幕上的图形并更改其大小或方向。

齐次坐标

为了执行一系列变换，例如先平移后旋转再缩放，我们需要遵循一个顺序过程：

平移坐标；
旋转平移后的坐标；然后
缩放旋转后的坐标以完成复合变换。

为了缩短此过程，我们必须使用3×3变换矩阵而不是2×2变换矩阵。为了将2×2矩阵转换为3×3矩阵，我们必须添加一个额外的虚拟坐标W。

通过这种方式，我们可以用3个数而不是2个数来表示点，这称为齐次坐标系统。在这个系统中，我们可以用矩阵乘法表示所有变换方程。任何笛卡尔点P(X, Y)都可以通过P’ (X_h, Y_h, h)转换为齐次坐标。

平移

平移将对象移动到屏幕上的不同位置。可以通过将平移坐标 (t_x, t_y) 添加到原始坐标 (X, Y) 来平移二维点，从而得到新的坐标 (X’, Y’)。

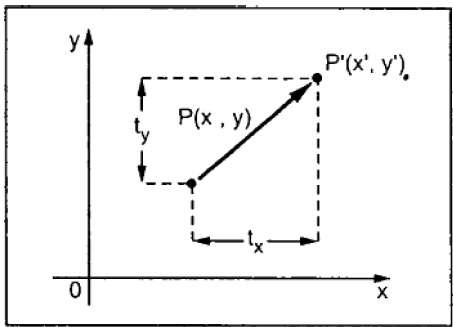
从上图可以看出：

X’ = X + t_x

Y’ = Y + t_y

对 (t_x, t_y) 称为平移向量或位移向量。上述方程也可以用列向量表示。

$P = \begin{bmatrix}X\\Y\end{bmatrix}$ p' = $\begin{bmatrix}X'\\Y'\end{bmatrix}$T = $\begin{bmatrix}t_{x}\\t_{y}\end{bmatrix}$

我们可以写成：

P’ = P + T

旋转

在旋转中，我们围绕其原点以特定角度 θ（theta）旋转对象。从下图可以看出，点 P(X, Y) 位于距原点距离为 r 的水平 X 坐标的角度 φ 处。

假设您想将其旋转角度 θ。旋转到新的位置后，您将得到一个新的点 P’ (X’, Y’)。

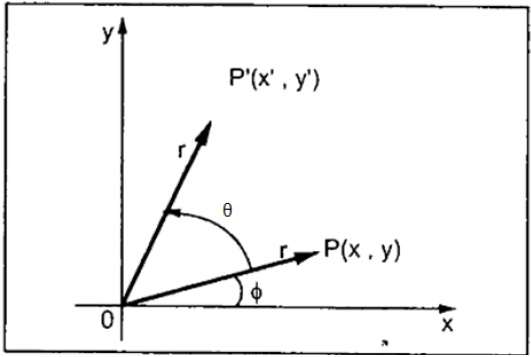
使用标准三角函数，点 P(X, Y) 的原始坐标可以表示为：

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

同样，我们可以表示点 P’ (X’, Y’) 为：

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$

将公式 (1) 和 (2) 分别代入 (3) 和 (4)，我们将得到

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

将上述方程表示为矩阵形式：

$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}OR $$

P’ = P . R

其中 R 是旋转矩阵

$$R = \begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$$

旋转角度可以为正也可以为负。

对于正旋转角度，我们可以使用上述旋转矩阵。但是，对于负角度旋转，矩阵将如下所示更改：

$$R = \begin{bmatrix} cos(-\theta) & sin(-\theta) \\ -sin(-\theta) & cos(-\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(-\theta ) = cos \theta \; and\; sin(-\theta ) = -sin \theta \right )$$

缩放

要更改对象的大小，可以使用缩放变换。在缩放过程中，您可以扩展或压缩对象的大小。可以通过将对象的原始坐标与缩放因子相乘来实现缩放，以获得所需的结果。

让我们假设原始坐标为 (X, Y)，缩放因子为 (S_X, S_Y)，产生的坐标为 (X’, Y’)。这可以用下面的数学公式表示：

X' = X . S_X 和 Y' = Y . S_Y

缩放因子 S_X、S_Y 分别沿 X 和 Y 方向缩放对象。上述方程也可以表示为以下矩阵形式：

$$ \begin{bmatrix} X' \\ Y' \end{bmatrix} = \begin{bmatrix} X \\ Y \end{bmatrix} \begin{bmatrix} S_{x} & 0 \\ 0 & S_{y} \end{bmatrix} $$

或

P’ = P . S

其中 S 是缩放矩阵。缩放过程如下图所示。

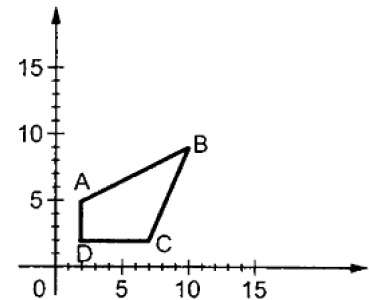
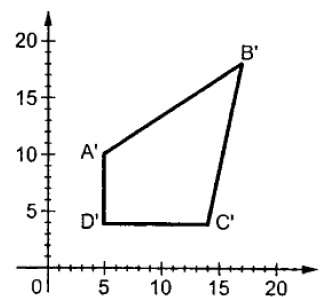
如果我们将小于 1 的值提供给缩放因子 S，则可以减小对象的大小。如果我们提供大于 1 的值，则可以增加对象的大小。

反射

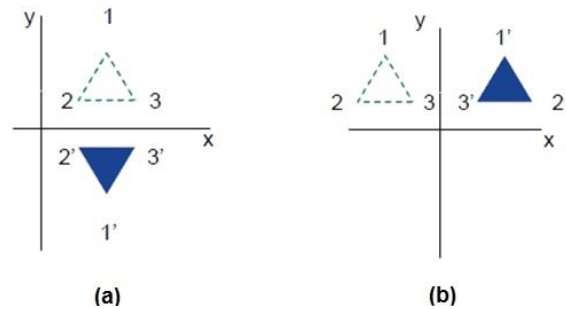
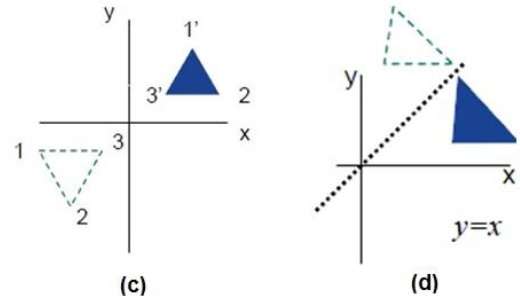
反射是原始对象的镜像。换句话说，我们可以说它是 180° 的旋转操作。在反射变换中，对象的大小不会改变。

下图分别显示了关于 X 轴和 Y 轴以及关于原点的反射。

剪切

使对象形状倾斜的变换称为剪切变换。有两种剪切变换：X 剪切和Y 剪切。一种会移动 X 坐标值，另一种会移动 Y 坐标值。但是，在这两种情况下，只有一个坐标会改变其坐标，而另一个坐标会保留其值。剪切也称为倾斜。

X 剪切

X 剪切保留 Y 坐标，并对 X 坐标进行更改，这会导致垂直线向左或向右倾斜，如下图所示。

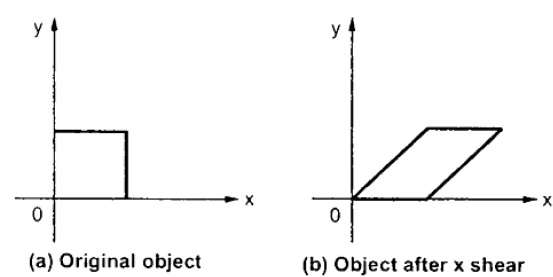
X 剪切的变换矩阵可以表示为：

$$X_{sh} = \begin{bmatrix} 1& shx & 0\\ 0& 1 & 0\\ 0& 0 & 1 \end{bmatrix}$$

Y' = Y + Sh_y . X

X’ = X

Y 剪切

Y 剪切保留 X 坐标并更改 Y 坐标，这会导致水平线转换为向上或向下倾斜的线，如下图所示。

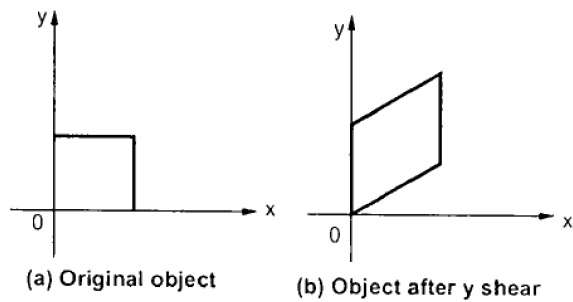
Y 剪切可以用矩阵表示为：

$$Y_{sh} \begin{bmatrix} 1& 0 & 0\\ shy& 1 & 0\\ 0& 0 & 1 \end{bmatrix}$$

X’ = X + Sh_x . Y

Y’ = Y

复合变换

如果平面 T1 的变换后接着是第二个平面变换 T2，则结果本身可以用单个变换 T 来表示，该变换是按该顺序组合 T1 和 T2 的结果。这写成 T = T1∙T2。

复合变换可以通过连接变换矩阵来实现，以获得组合变换矩阵。

组合矩阵：

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

其中 [Ti] 是任何组合

平移
缩放
剪切
旋转
反射

变换顺序的变化会导致不同的结果，因为通常矩阵乘法不是累积的，即 [A] . [B] ≠ [B] . [A]，以及乘法的顺序。组合变换的基本目的是通过将单个组合变换应用于点来提高效率，而不是一个接一个地应用一系列变换。

例如，要围绕任意点 (X_p, Y_p) 旋转对象，我们必须执行三个步骤：

将点 (X_p, Y_p) 平移到原点。
围绕原点旋转它。
最后，将旋转中心移回它所属的位置。

打印页面